Question

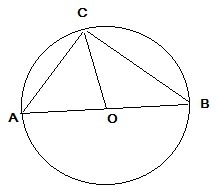
В окружности с центром О проведены диаметр AB и хорда AC Докажите что угол C A B равен 1/2 угла C О B

Answer 1

1 способ. ∠САВ-вписанный, опирается на дугу СВ,
по свойству вписанного угла он равен 1/2 ∪СВ.
∠СОВ-центральный, опирается на дугу СВ,
по свойству центрального угла он равен ∪СВ,
значит 
∠САВ=1/2∠СОВ.
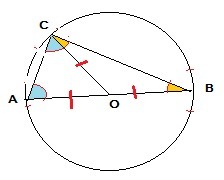
2 способ.
АО=СО=ОВ-как радиусы одной окружности.
Тогда ∠АОС=180-2∠САВ⇒
∠СОВ=180-∠АОС=180-(180-2∠САВ)=180-180+2∠САВ=2∠САВ⇒
∠САВ=1/2∠СОВ
Прикреплен еще один рисунок.