Предмет: Алгебра,
автор: hykzip
Степень с целым показателем
Приложения:
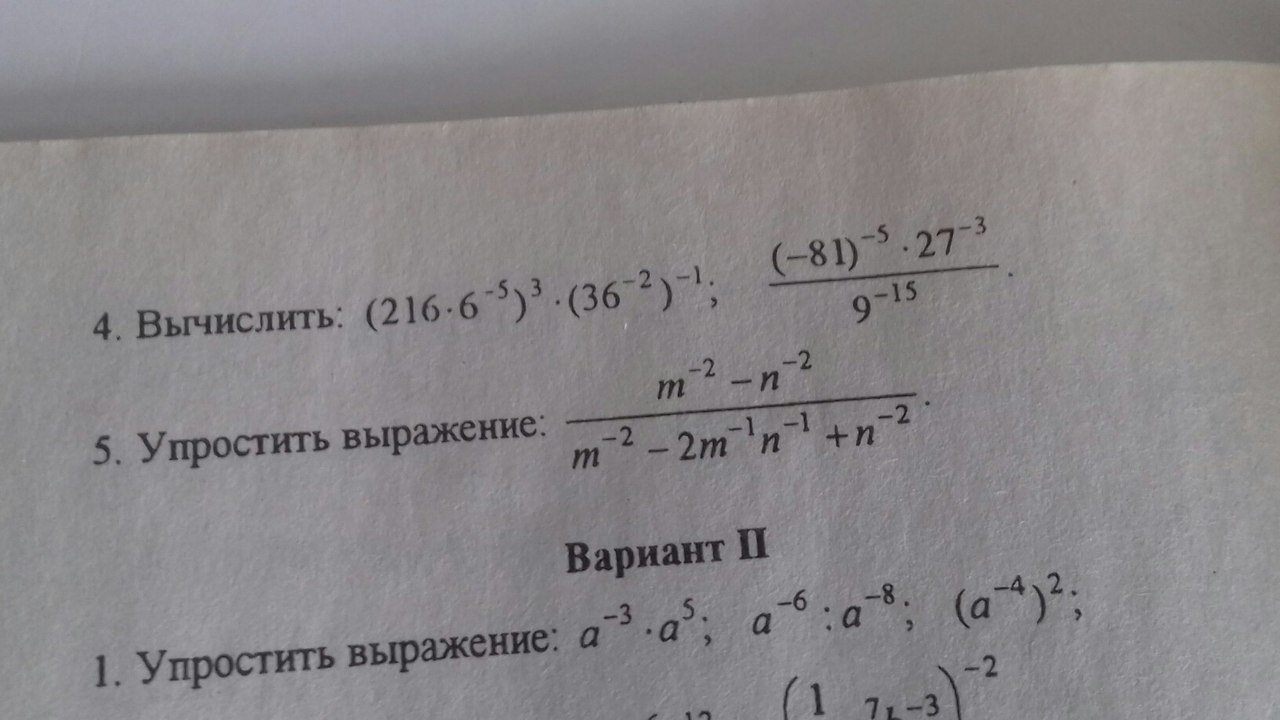
MizoriesKun:
какое ?
4 5
Ответы
Автор ответа:
0
Если вдруг что-то не так то прости
Приложения:


Автор ответа:
0
Похожие вопросы
Предмет: Геометрия,
автор: mikolaskvirskij1
Предмет: Математика,
автор: reginas59
Предмет: Геометрия,
автор: dimareznikov09
Предмет: Математика,
автор: vodrink