Предмет: Алгебра,
автор: Машка1357
помогите 1 задание пожалуйста
Приложения:
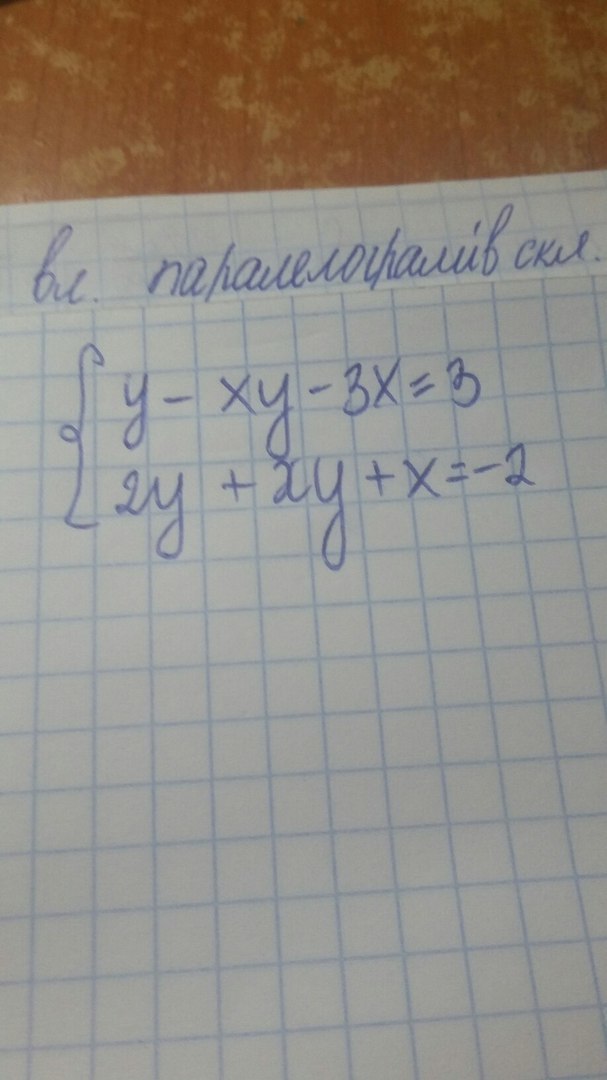
Ответы
Автор ответа:
1
Первое плюс второе. Выбираем любое и решаем способом подстановки. Далее квадратное уравнение и видим, что это квадрат суммы. Всё коротко и просто. Решение задания приложено
Приложения:

Автор ответа:
1
Ответ:
Машка1357:
я поняла как решать спасибо!!!
пожалуйста
Похожие вопросы
Предмет: Математика,
автор: alisa2338
Предмет: Информатика,
автор: tegnichosi
Предмет: Математика,
автор: diana040874
Предмет: География,
автор: aidaenis
Предмет: Биология,
автор: alene2013meco