Предмет: Геометрия,
автор: klimenkol21
Помогите с геометрией:
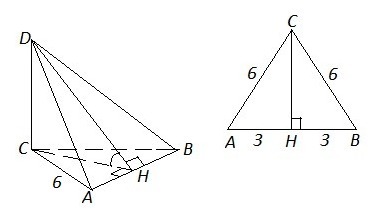
Ребро CD треугольной пирамиды ABCD перпендикулярно к плоскости АВС. Найдите друхгранные углы DACB, DABC, BDCA, если АВ=ВС=АС=6 и BD=3√7
Ответы
Автор ответа:
1
Чтобы определить линейный угол двугранного угла, надо к линии пересечения плоскостей (граней угла) провести перпендикуляры в обеих плоскостях. Угол между проведёнными перпендикулярами и будет искомым углом. Удобно, когда перпендикуляры проводятся из одной точки,лежащей на линии пересечения.Определим линейный угол двугранного угла DABС. Линия пересечения плоскостей - АВ. Точка D лежит в пл. АВD , а точка С - в пл. АВС. Проведём СH⊥AB в пл АВС ⇒ СH явл. перпендикуляром в пл. AВС к АВ. СH явл. также биссектрисой и медианой, т.к. ΔАВС равносторонний, все его стороны = 6 , ВН=6:2=3, СН=√(АС²-АН²)=√(6²-3²)=√(36-9)=√27=√(9·3)=3√3 .
Соединим точку D и Н. DH - наклонная, DС - перпендикуляр к пл. АВС ⇒СН - проекция наклонной DH на пл. АВС. Т.к. проекция СН ⊥АВ ⇒ по теореме о трёх перпендикулярах тогда и наклонная DH⊥AB. DH явл. перпендикуляром к АВ в пл. ABD.Найдём DН из ΔABD. ⇒ DH=√(DB²-BH²)=√((3·√7)²-3²)=√(9·7-9)=√54=√(9·6)=3√6 .
Получили, что DH⊥AB и CH⊥AB ⇒ линейный ∠DHC - есть линейный угол двугранного угла DABC. (Из сказанного следует ещё,что AB⊥пл.DCH)∠DHC найдём из ΔDCH. ∠DCH=90°, cos∠DHC=CH/DH=(3√3)/(6√3)=√(3/6)=√(1/2)=1/√2=√2/2 ⇒ ∠DHC=45°.
Двугранному углу DACB соответcтвует линейный угол DCB, т.к. пл.ВАС перпендикулярна пл.DAC , то ∠DCB=90°.
Двугранному углу BDCA соответствует линейный ∠АСВ, т.к. DС⊥AC и DC⊥BC.∠АСВ=60° как угол равностороннего треугольника .
Ответ: 90° , 45° , 60° .
Соединим точку D и Н. DH - наклонная, DС - перпендикуляр к пл. АВС ⇒СН - проекция наклонной DH на пл. АВС. Т.к. проекция СН ⊥АВ ⇒ по теореме о трёх перпендикулярах тогда и наклонная DH⊥AB. DH явл. перпендикуляром к АВ в пл. ABD.Найдём DН из ΔABD. ⇒ DH=√(DB²-BH²)=√((3·√7)²-3²)=√(9·7-9)=√54=√(9·6)=3√6 .
Получили, что DH⊥AB и CH⊥AB ⇒ линейный ∠DHC - есть линейный угол двугранного угла DABC. (Из сказанного следует ещё,что AB⊥пл.DCH)∠DHC найдём из ΔDCH. ∠DCH=90°, cos∠DHC=CH/DH=(3√3)/(6√3)=√(3/6)=√(1/2)=1/√2=√2/2 ⇒ ∠DHC=45°.
Двугранному углу DACB соответcтвует линейный угол DCB, т.к. пл.ВАС перпендикулярна пл.DAC , то ∠DCB=90°.
Двугранному углу BDCA соответствует линейный ∠АСВ, т.к. DС⊥AC и DC⊥BC.∠АСВ=60° как угол равностороннего треугольника .
Ответ: 90° , 45° , 60° .
Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: Hhfugb
Предмет: Математика,
автор: alionabogdanovich09
Предмет: Геометрия,
автор: mast597
Предмет: Литература,
автор: ольга325
Предмет: Математика,
автор: Николай831