Предмет: Алгебра,
автор: xQx
помогите пж
1 неравенство
задание на фото
Приложения:
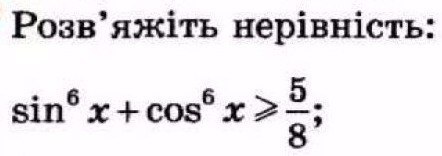
Ответы
Автор ответа:
6
Похожие вопросы
Предмет: История,
автор: sampserveramaks
Предмет: Другие предметы,
автор: inessamel08
Предмет: Физика,
автор: Fenixb
Предмет: Математика,
автор: Yliopkd
Предмет: Литература,
автор: protsenkomisa