Предмет: Математика,
автор: hikkimorri
А)сos x > √2/2 (решите неравенство с помощью окружности) б)tg x < √3 (решите неравенство с помощью окружности)
Ответы
Автор ответа:
1
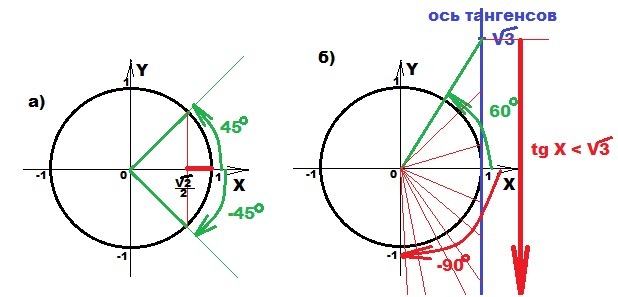
А) сos x > √2/2
cos α - это проекция на ось OX радиуса единичной окружности, образующего угол α с положительным направлением оси OX.
-1 ≤ cos α ≤ 1
cos x = √2/2 - табличный косинус угла 45° = π/4
Функция y = cos x - чётная и имеет период 360° = 2π
Симметричное значение косинуса:
cos(-45°) = cos(-π/4)=√2/2
Для решения неравенства сos x > √2/2 подойдут значения углов
-45° + 360°n < x < 45° + 360°n или
-π/4 + 2πn < x < π/4 + 2πn, n∈Z
x ∈ (-π/4 + 2πn; π/4 + 2πn), n∈Z
б) tg x < √3
Значения тангенса угла находят с помощью прямой x=1, называемой осью тангенсов. Для этого радиус единичной окружности, образующий угол α с положительным направлением оси OX, продлевают до пересечения с осью тангенсов. Ордината точки пересечения и будет значением tgα.
tg x = √3 - табличное значение тангенса для угла 60° = π/3
Функция tg α монотонно возрастающая и имеет период 180° = π.
Для решения неравенства tg x < √3 подойдут углы, тангенсы которых расположены на оси тангенсов ниже числа √3 :
-90° + 180°k < x < 60° + 180°k или
-π/2 + πk < x < π/3 + πk, k∈Z
x ∈ (-π/2 + πk; π/3 + πk), k∈Z
cos α - это проекция на ось OX радиуса единичной окружности, образующего угол α с положительным направлением оси OX.
-1 ≤ cos α ≤ 1
cos x = √2/2 - табличный косинус угла 45° = π/4
Функция y = cos x - чётная и имеет период 360° = 2π
Симметричное значение косинуса:
cos(-45°) = cos(-π/4)=√2/2
Для решения неравенства сos x > √2/2 подойдут значения углов
-45° + 360°n < x < 45° + 360°n или
-π/4 + 2πn < x < π/4 + 2πn, n∈Z
x ∈ (-π/4 + 2πn; π/4 + 2πn), n∈Z
б) tg x < √3
Значения тангенса угла находят с помощью прямой x=1, называемой осью тангенсов. Для этого радиус единичной окружности, образующий угол α с положительным направлением оси OX, продлевают до пересечения с осью тангенсов. Ордината точки пересечения и будет значением tgα.
tg x = √3 - табличное значение тангенса для угла 60° = π/3
Функция tg α монотонно возрастающая и имеет период 180° = π.
Для решения неравенства tg x < √3 подойдут углы, тангенсы которых расположены на оси тангенсов ниже числа √3 :
-90° + 180°k < x < 60° + 180°k или
-π/2 + πk < x < π/3 + πk, k∈Z
x ∈ (-π/2 + πk; π/3 + πk), k∈Z
Приложения:
Похожие вопросы
Предмет: Математика,
автор: mica81
Предмет: Алгебра,
автор: TR3D0W
Предмет: Математика,
автор: martalibini
Предмет: Музыка,
автор: eseniyakovalev