Предмет: Математика,
автор: 1313ff
Правило Лопиталя. Вычислить пределы
Приложения:
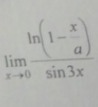
Ответы
Автор ответа:
0
По правилу лопиталя
Похожие вопросы
Предмет: История,
автор: Аноним
Предмет: Математика,
автор: zaitovam0
Предмет: Математика,
автор: muuushromik
Предмет: Математика,
автор: lil39