Question

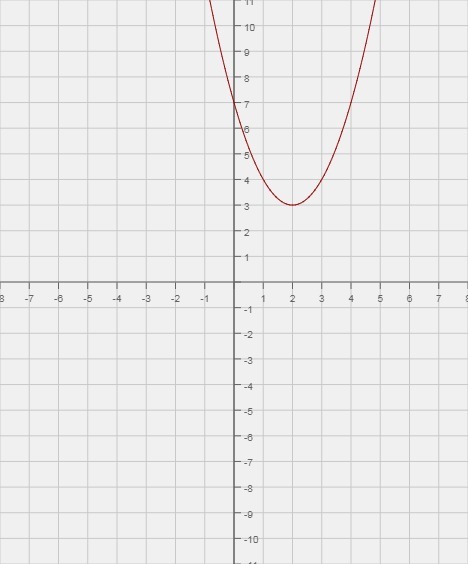
Для параболы y=(x-2)^+3:
а) координаты вершины параболы;
Б) направление ветвей

Answer 1

$y=(x-2)^2+3$
I способ
Для облегчения преобразуем, хотя можно работать и с такой функцией
$y=x^2-4x+7$
$a \ \textgreater \ 0$ ⇒ ветви параболы смотрят вверх
Находим координаты вершины параболы:
$x_0 = \frac{-b}{2a} \Rightarrow x_0 = \frac{4}{2} = 2 \\ \\ y_0 = 2^2-4\cdot2+7 = 3$
II способ
$y=(x-2)^2+3$
Данная функция является функцией вида $y=a(x-m)^2+n$
$(m;n)$ - координаты вершины параболы 
Следовательно, вершина параболы имеет точки $(2;3)$, а ветви смотрят вверх, т.к. $a \ \textgreater \ 0$