Предмет: Алгебра,
автор: SLI2000a
Помогите пожалуйста решить первое уравнение
Приложения:
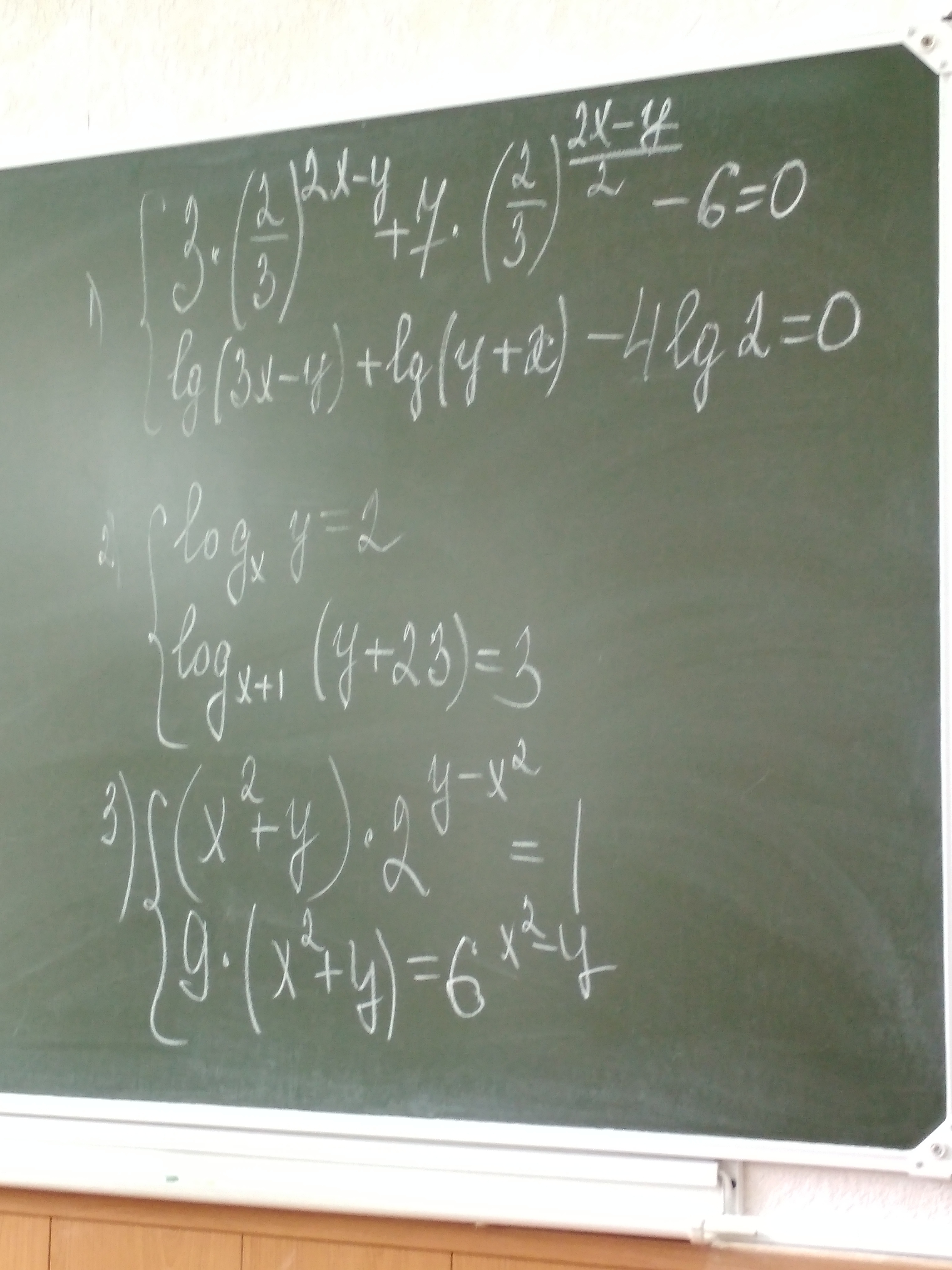
Ответы
Автор ответа:
1
Решим первое уравнение, сделав замену:
 не подходит
не подходит

Решим второе уравнение:
ОДЗ: 1) 3x-y > 0 ⇒ y < 3x
2) y + x > 0 ⇒ y > - x

Ответ: (2;2) ,
Решим второе уравнение:
ОДЗ: 1) 3x-y > 0 ⇒ y < 3x
2) y + x > 0 ⇒ y > - x
Ответ: (2;2) ,
SLI2000a:
Спасибо вам большое)
Пожалуйста
Похожие вопросы
Предмет: Математика,
автор: arinakozlova1704
Предмет: Русский язык,
автор: polakovaola421
Предмет: Химия,
автор: ddv1303
Предмет: Математика,
автор: vlad54211