Предмет: Алгебра,
автор: Кариночка78
Распишите, пожалуйста, подробно решение неравенства. Если можно, то с ОДЗ
Приложения:
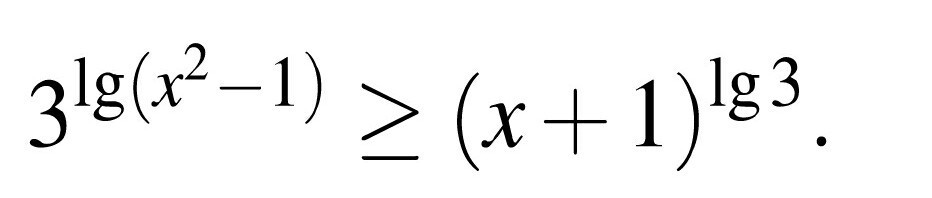
мне нужно другое решение
Ответы
Автор ответа:
0
3^(lg(x^2 - 1) >= (x+1)^lg (3)
ОДЗ
x^2-1>0 (как основание логарифма) (x-1)(x+1)>0 x∈(-∞ -1) U (1 +∞)
x+1>0 (возводить отрицательные числа в нецелые степени на поле действительных чисел нельзя) x>-1
Итак x∈(1 +∞)
вспомним свойство логарифма a^log(b) c = c^ log(b) a и применим к правой части
3 ^ lg(x^2 - 1) >= (x+1)^lg (3)
3 ^ lg(x^2 - 1) >= 3 ^ lg (x+1)
lg(x^2 - 1) >= lg(x+1)
(x+1)(x-1) >= x+1
(x+1)(x-1) - (x+1) >=0
(x+1)(x-2)>=0
метод интервалов
+++++++ [-1] --------- [2] ++++++
x∈(- ∞ -1] U [2 +∞)
пересекаем с ОДЗ
и получаем x∈ [2 +∞)
ОДЗ
x^2-1>0 (как основание логарифма) (x-1)(x+1)>0 x∈(-∞ -1) U (1 +∞)
x+1>0 (возводить отрицательные числа в нецелые степени на поле действительных чисел нельзя) x>-1
Итак x∈(1 +∞)
вспомним свойство логарифма a^log(b) c = c^ log(b) a и применим к правой части
3 ^ lg(x^2 - 1) >= (x+1)^lg (3)
3 ^ lg(x^2 - 1) >= 3 ^ lg (x+1)
lg(x^2 - 1) >= lg(x+1)
(x+1)(x-1) >= x+1
(x+1)(x-1) - (x+1) >=0
(x+1)(x-2)>=0
метод интервалов
+++++++ [-1] --------- [2] ++++++
x∈(- ∞ -1] U [2 +∞)
пересекаем с ОДЗ
и получаем x∈ [2 +∞)
Автор ответа:
0
Решение задания приложено
Приложения:

Похожие вопросы
Предмет: Физика,
автор: artemovamasa6
Предмет: Математика,
автор: Аноним
Предмет: Русский язык,
автор: shskinas
Предмет: Математика,
автор: agradina
Предмет: Математика,
автор: egorrka1
если то хотя бы разбирали, то и это решите