Предмет: Алгебра,
автор: 6ViShy6
Помогите решить неравенство
Приложения:
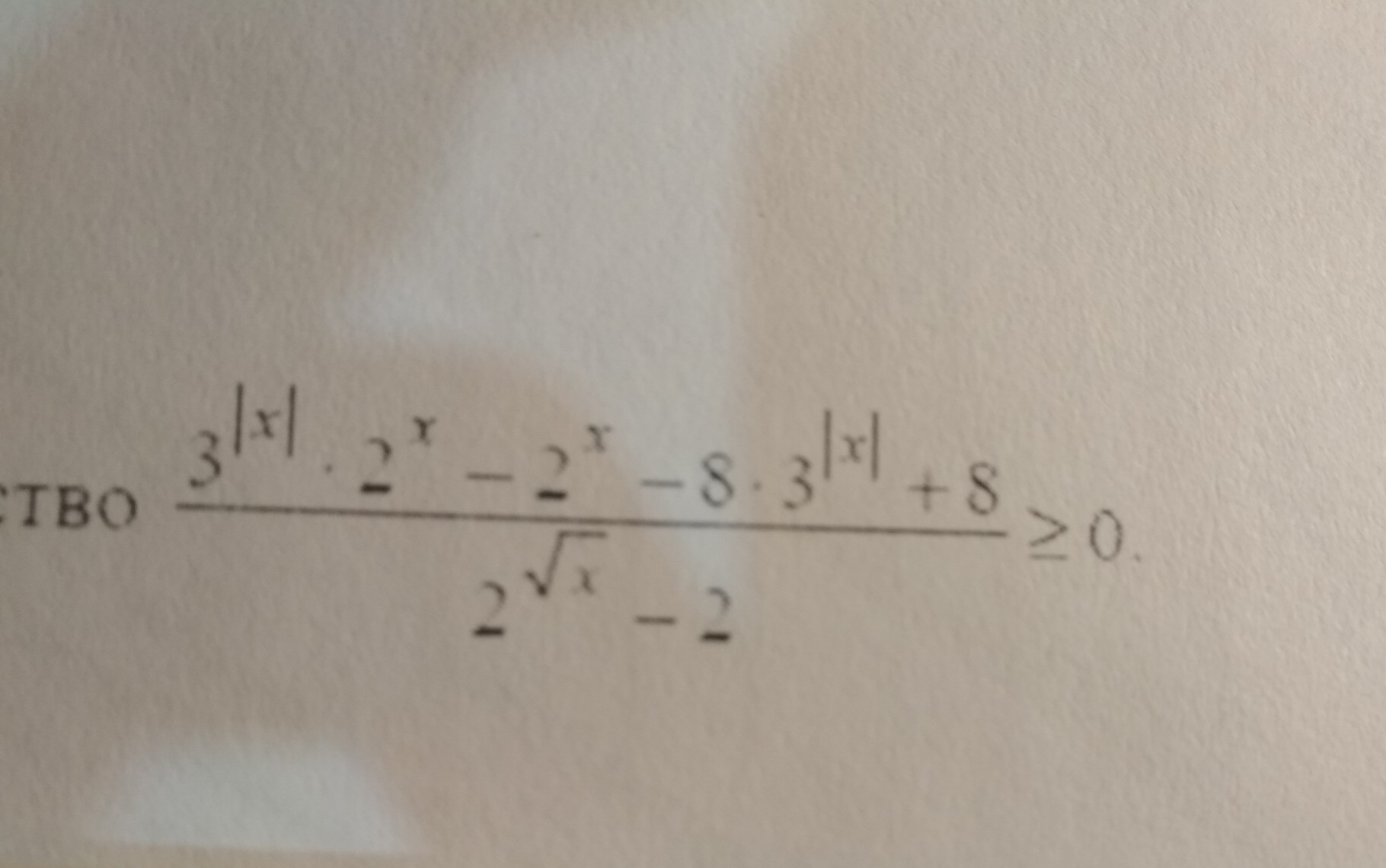
Ответы
Автор ответа:
2
если
Значит
--------------------------
если
второй и первый случаи вместе дают:
Ответ:
Похожие вопросы
Предмет: Математика,
автор: demtyk2002
Предмет: Французский язык,
автор: MiceVX
Предмет: Информатика,
автор: obervanukveronika
Предмет: Математика,
автор: фрост20
Предмет: Математика,
автор: samsa89