Предмет: Математика,
автор: Needyourhelpbro
упростить выражение рис.1, получается то, что на рис. 2. Каким образом, что-то понять не могу.
Приложения:
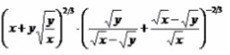
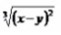
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Другие предметы,
автор: vasaputilov84341
Предмет: Физика,
автор: elizavetazemcova286
Предмет: Другие предметы,
автор: angelinakryvko
Предмет: Математика,
автор: михаил601
Предмет: Литература,
автор: Ангелина1000007