Question

Дан треугольник ABC с прямым углом B. Найдите длину медианы BM, если:

a) AC=10 см

Answer 1

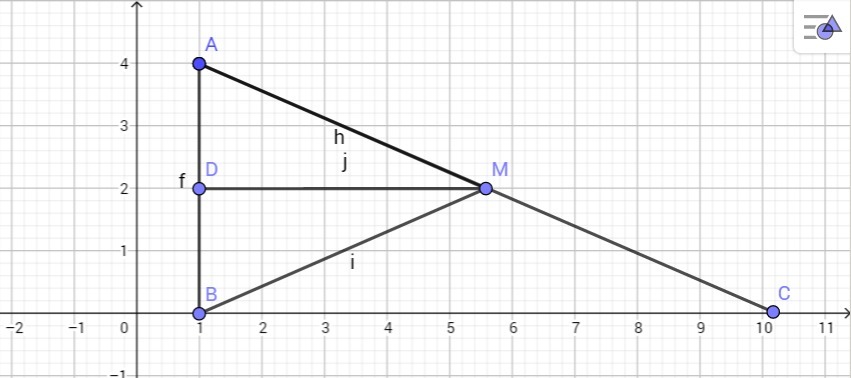
Опустим перпендикуляр MD из точки M на сторону AB.

Параллельные прямые, отсекающие пропорциональные отрезки на одной стороне (AC) угла (<BAC), отсекают пропорциональные отрезки и на второй (AB) его стороне (теорема о пропорциональных отрезках).

Так как АМ = МС, то и AD = DB.

Треугольники ADM и BDM равны по первому признаку равенства (сторона DM - общая, углы ADM и BDM равны по 90 градусов, т. к. DM - это перпендикуляр, стороны AD и DB равны).

Значит и BM = AM = 10 см /2 = 5 см

Ответ: 5 см