Question

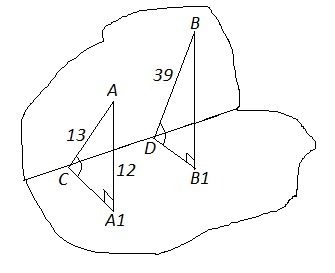
1.) На одной из граней угла лежат две точки А и В удалённые от ребра на 13 см и 39 см соответственно . Найти расстояние от точки В до другой грани , если точка А удалена от нее ( грани ) на 12 см .
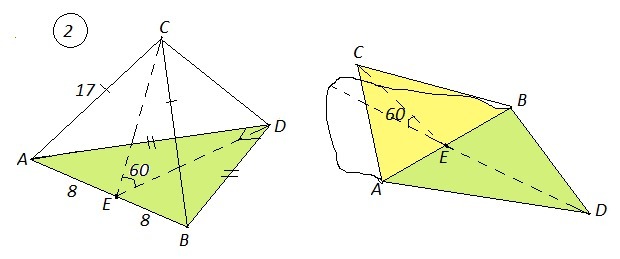
2.) Равнобедренные треугольники АВС и АВД с общим основанием АВ = 16 см , лежат в разных плоскостях угол между , которыми = 60 градусов . Найти расстояние между вершинами треугольников , если АС = СВ = 17 см , АД перпендикулярно ВД .

Answer 1

1)  АС=13 ,  ВD=39 ,  AA1=12
  sinACA1=12/13 =sinBDB1
BB1=BD*sinBDB1=39*(12/13)=36
2)  a)   Проведём СЕ⊥АВ и DE⊥AB. 
АЕ=ВЕ=1/2*АВ=1/2*16=8 , т.к. АВС - равнобедренный, Е - середина АВ.
 DE - тоже высота , медиана и биссектриса, т.к. АВD - равнобедренный, AD=BD.
СЕ²=АС²-АЕ²=17²-8²=225 ,  СЕ=15
∠ADB=90° по условию, ∠BDE=45°  ⇒  ∠DBE=45°  ⇒  ΔBDE - равнобедренный,  DE=BE=8 .
ΔCDE:  CE⊥AB и DE⊥AB  ⇒  ∠CED=60° ,
 CD²=CE²+DE²-2*CE*DE*cos60°=15²+8²-2*15*8*0,5=169
CD=13
б)  ∠СD=180°-60°=120°  ⇒ 
CD²=15²+8²-2*15*8*cos120°=15²+8²+2*15*8*0,5=409
CD=√409
Ответ:  13 или √409.

Answer 2

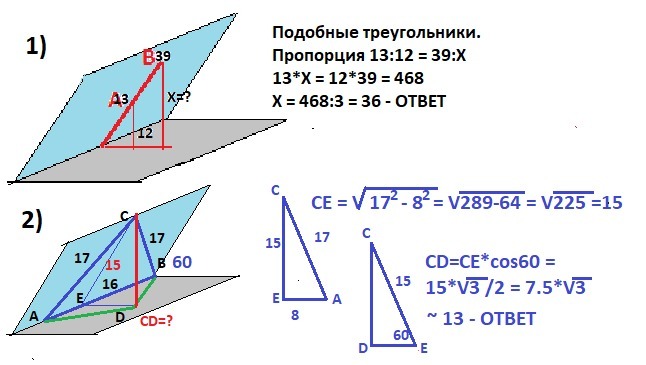
РЕШЕНИЕ задач на рисунке в приложений.
Задача 1 - подобные треугольники - пропорция.
Задача 2 - по т. Пифагора с использованием функции косинус.
ОТВЕТ на рисунке в приложении.