Предмет: Математика,
автор: 1997zhenya
ИССЛЕДОВАТЬ ФУНКЦИЮ НА НЕПРЕРЫВНОСТЬ
Приложения:
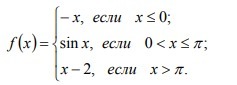
Ответы
Автор ответа:
0
Сами по себе функции f₁(x)=-x; f₂(x)=sin(x); f₃(x)=x-2 непрерывны при x ∈ R. ⇔
⇔ На любом открытом интервале вида ]a;b[ , где a<b ∧ a,b ∈ R любая из этих функций непрерывна. ⇒
⇒ Непрерывность функции f(x) может быть нарушена только в точках которые задают частичную область определения функций f₁(x); f₂(x); f₃(x) как минимум в двух функциях.
D(f₁) = ]-∞;0]
D(f₂) = ]0;π]
D(f₃) = ]π;∞[
Видно, что существует две такие точки, а именно (0;f(0)); (π;f(π))
Для того, чтобы исследовать функцию f(x) на непрерывность достаточно исследовать её на непрерывность в этих двух точках.
 ~
~  ⇒
⇒
⇒f непрерывна в точке (0;f(0))
 ⇒
⇒
⇒f не непрерывна в точке (π;f(π))
Исследование функции f на непрерывность показало, что в точке (π;f(π)) функция терпит неустранимый разрыв первого рода (по определению) из чего следует, что она не непрерывна на своей области определения.
⇔ На любом открытом интервале вида ]a;b[ , где a<b ∧ a,b ∈ R любая из этих функций непрерывна. ⇒
⇒ Непрерывность функции f(x) может быть нарушена только в точках которые задают частичную область определения функций f₁(x); f₂(x); f₃(x) как минимум в двух функциях.
D(f₁) = ]-∞;0]
D(f₂) = ]0;π]
D(f₃) = ]π;∞[
Видно, что существует две такие точки, а именно (0;f(0)); (π;f(π))
Для того, чтобы исследовать функцию f(x) на непрерывность достаточно исследовать её на непрерывность в этих двух точках.
⇒f непрерывна в точке (0;f(0))
⇒f не непрерывна в точке (π;f(π))
Исследование функции f на непрерывность показало, что в точке (π;f(π)) функция терпит неустранимый разрыв первого рода (по определению) из чего следует, что она не непрерывна на своей области определения.
Похожие вопросы
Предмет: Русский язык,
автор: ruslan42946
Предмет: Русский язык,
автор: dinaed45
Предмет: Математика,
автор: abdurahimovasabina2
Предмет: Математика,
автор: Викуля55555
Предмет: Математика,
автор: elenaleyn