Предмет: Математика,
автор: grebenshikova21
Вычислить пределы не используя правило Лопиталя
Распишите пожалуйста
Приложения:
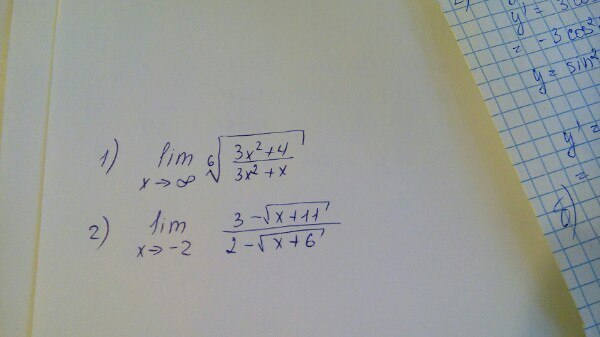
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: av8167617
Предмет: Математика,
автор: Аноним
Предмет: Физика,
автор: alicedanilevskaya
Предмет: Математика,
автор: kraynova04
Предмет: Литература,
автор: пузяка1