Предмет: Алгебра,
автор: liza22225
как тут находят производную, я не понимаю...по каким формулам?
Приложения:
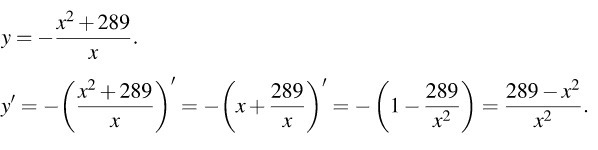
Ответы
Автор ответа:
1
по формулам:
![1)\ \ [u+v]'=u'+v'\\\\
2)\ \ (x^a)'=a*x^{a-1}\\\\
(x)'=(x^1)=1*x^{1-1}=1*x^0=1*1=1\\\\
(\frac{1}{x})'=(x^{-1})'=-1*x^{-1-1}=-x^{-2}=-\frac{1}{x^2}\\\\
3)\ \ [c*f(x)]'=c*[f(x)]'=c*f'(x)\\\\
------------------------------\\\\
(\frac{289}{x})'=(289*\frac{1}{x})'=289*(\frac{1}{x})'=289*(-\frac{1}{x^2})=-\frac{289}{x^2}\\\\
y(x)=-\frac{x^2+289}{x}=-(\frac{x^2}{x}+\frac{289}{x})=-(x+\frac{289}{x})=(-1)*(x+\frac{289}{x})\\\\
y'(x)=[(-1)*(x+\frac{289}{x})]'=(-1)*[x+\frac{289}{x}]'=\\\\](https://tex.z-dn.net/?f=1%29%5C+%5C+%5Bu%2Bv%5D%27%3Du%27%2Bv%27%5C%5C%5C%5C%0A2%29%5C+%5C+%28x%5Ea%29%27%3Da%2Ax%5E%7Ba-1%7D%5C%5C%5C%5C%0A%28x%29%27%3D%28x%5E1%29%3D1%2Ax%5E%7B1-1%7D%3D1%2Ax%5E0%3D1%2A1%3D1%5C%5C%5C%5C%0A%28%5Cfrac%7B1%7D%7Bx%7D%29%27%3D%28x%5E%7B-1%7D%29%27%3D-1%2Ax%5E%7B-1-1%7D%3D-x%5E%7B-2%7D%3D-%5Cfrac%7B1%7D%7Bx%5E2%7D%5C%5C%5C%5C%0A3%29%5C+%5C+%5Bc%2Af%28x%29%5D%27%3Dc%2A%5Bf%28x%29%5D%27%3Dc%2Af%27%28x%29%5C%5C%5C%5C%0A------------------------------%5C%5C%5C%5C%0A%28%5Cfrac%7B289%7D%7Bx%7D%29%27%3D%28289%2A%5Cfrac%7B1%7D%7Bx%7D%29%27%3D289%2A%28%5Cfrac%7B1%7D%7Bx%7D%29%27%3D289%2A%28-%5Cfrac%7B1%7D%7Bx%5E2%7D%29%3D-%5Cfrac%7B289%7D%7Bx%5E2%7D%5C%5C%5C%5C%0Ay%28x%29%3D-%5Cfrac%7Bx%5E2%2B289%7D%7Bx%7D%3D-%28%5Cfrac%7Bx%5E2%7D%7Bx%7D%2B%5Cfrac%7B289%7D%7Bx%7D%29%3D-%28x%2B%5Cfrac%7B289%7D%7Bx%7D%29%3D%28-1%29%2A%28x%2B%5Cfrac%7B289%7D%7Bx%7D%29%5C%5C%5C%5C%0Ay%27%28x%29%3D%5B%28-1%29%2A%28x%2B%5Cfrac%7B289%7D%7Bx%7D%29%5D%27%3D%28-1%29%2A%5Bx%2B%5Cfrac%7B289%7D%7Bx%7D%5D%27%3D%5C%5C%5C%5C "1)\ \ [u+v]'=u'+v'\\\\
2)\ \ (x^a)'=a*x^{a-1}\\\\
(x)'=(x^1)=1*x^{1-1}=1*x^0=1*1=1\\\\
(\frac{1}{x})'=(x^{-1})'=-1*x^{-1-1}=-x^{-2}=-\frac{1}{x^2}\\\\
3)\ \ [c*f(x)]'=c*[f(x)]'=c*f'(x)\\\\
------------------------------\\\\
(\frac{289}{x})'=(289*\frac{1}{x})'=289*(\frac{1}{x})'=289*(-\frac{1}{x^2})=-\frac{289}{x^2}\\\\
y(x)=-\frac{x^2+289}{x}=-(\frac{x^2}{x}+\frac{289}{x})=-(x+\frac{289}{x})=(-1)*(x+\frac{289}{x})\\\\
y'(x)=[(-1)*(x+\frac{289}{x})]'=(-1)*[x+\frac{289}{x}]'=\\\\")
![=-[(x)'+(\frac{289}{x})']=-[1+(-\frac{289}{x^2})]=\\\\
=-[1-\frac{289}{x^2}]=-[\frac{x^2}{x^2}-\frac{289}{x^2}]=-[\frac{x^2-289}{x^2}]=-\frac{x^2-289}{x^2}=\\\\
=\frac{-(x^2-289)}{x^2}=\frac{-x^2+289}{x^2}=\frac{289-x^2}{x^2}](https://tex.z-dn.net/?f=%3D-%5B%28x%29%27%2B%28%5Cfrac%7B289%7D%7Bx%7D%29%27%5D%3D-%5B1%2B%28-%5Cfrac%7B289%7D%7Bx%5E2%7D%29%5D%3D%5C%5C%5C%5C%0A%3D-%5B1-%5Cfrac%7B289%7D%7Bx%5E2%7D%5D%3D-%5B%5Cfrac%7Bx%5E2%7D%7Bx%5E2%7D-%5Cfrac%7B289%7D%7Bx%5E2%7D%5D%3D-%5B%5Cfrac%7Bx%5E2-289%7D%7Bx%5E2%7D%5D%3D-%5Cfrac%7Bx%5E2-289%7D%7Bx%5E2%7D%3D%5C%5C%5C%5C%0A%3D%5Cfrac%7B-%28x%5E2-289%29%7D%7Bx%5E2%7D%3D%5Cfrac%7B-x%5E2%2B289%7D%7Bx%5E2%7D%3D%5Cfrac%7B289-x%5E2%7D%7Bx%5E2%7D "=-[(x)'+(\frac{289}{x})']=-[1+(-\frac{289}{x^2})]=\\\\
=-[1-\frac{289}{x^2}]=-[\frac{x^2}{x^2}-\frac{289}{x^2}]=-[\frac{x^2-289}{x^2}]=-\frac{x^2-289}{x^2}=\\\\
=\frac{-(x^2-289)}{x^2}=\frac{-x^2+289}{x^2}=\frac{289-x^2}{x^2}")
Похожие вопросы
Предмет: Алгебра,
автор: tiwnit70
Предмет: Алгебра,
автор: Getooo
Предмет: Русский язык,
автор: taya8girl
Предмет: Литература,
автор: fksb
Предмет: Математика,
автор: Аничка20