Предмет: Алгебра,
автор: Анна5151515
Докажите, пожалуйста, тождество.
Приложения:
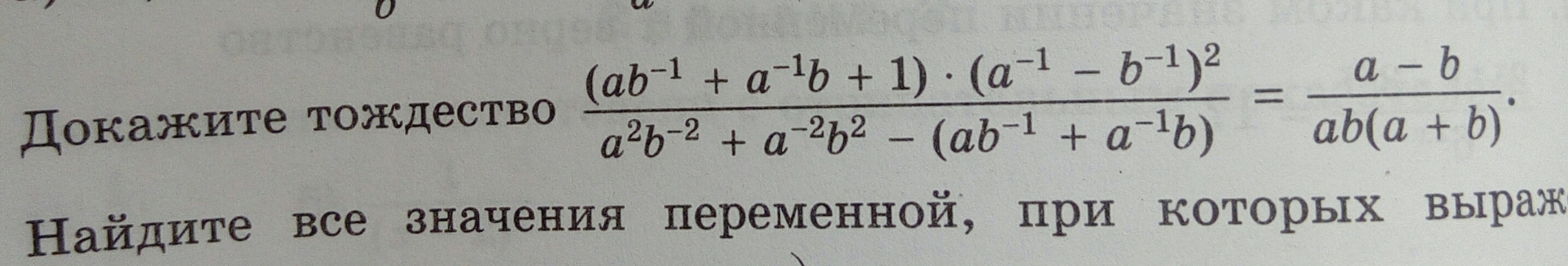
Ответы
Автор ответа:
1
Если бы в условии в знаменателе вместо
то действительно, ответ получился бы
Похожие вопросы
Предмет: Математика,
автор: marmeladka282
Предмет: Английский язык,
автор: ahmedovamaram65
Предмет: Русский язык,
автор: dilya8689
Предмет: Математика,
автор: yoush01
Предмет: Математика,
автор: Samir4555