Предмет: Алгебра,
автор: Аля1315
Помогите, пожалуйста, решить уравнения.
Приложения:
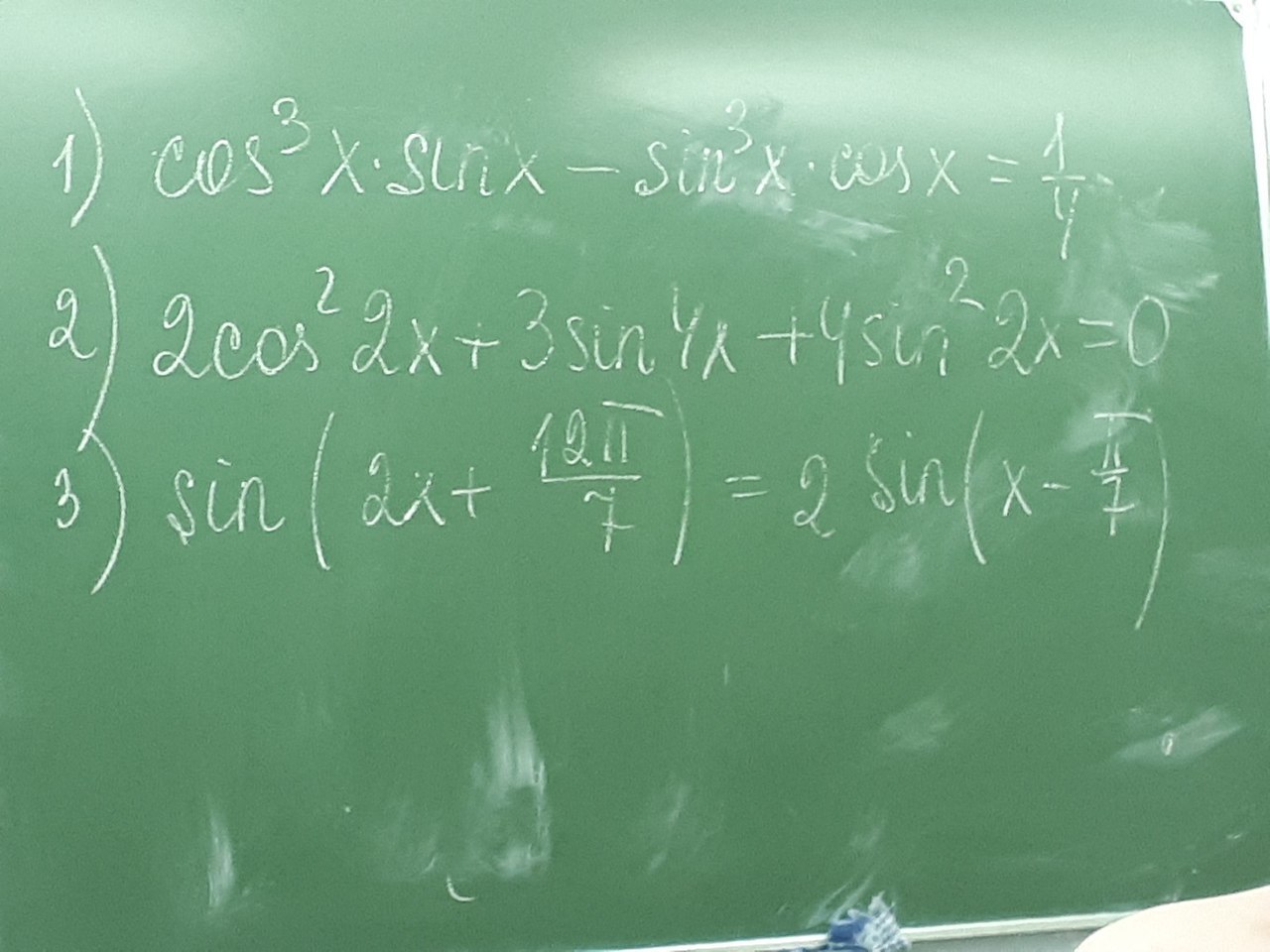
Ответы
Автор ответа:
0
Решение
1) sin³x*cosx - cos³x*sinx = 1/4
Умножим обе части уравнения на 4
4*(sin³x*·cosx - cos³x*sinx) = 1
4*(sin²x*sinx*cosx-cos²x*cosx*sinx) = 1
4*sinx*cosx*(sin²x - cos²x) = 1
- 2*(2*sinx*cosx)*(cos²x - sin²x) = 1
- 2*sin2x*cos2x = 1
- sin4x = 1
sin4x= - 1
4x = - π/2 + 2πk, k∈Z
x = - π/8 + πk/2, k∈Z
2) 2cos²2x + 3*2*sin2xcos2x + 4sin²2x = 0
2cos²2x +6sin2xcos2x + 4sin²2x = 0
делим на cos²2x ≠ 0
4tg²2x + 6tg2x + 2 = 0
делим на 2
2tg²2x +3tg2x + 1 = 0
tg2x = t
2t² + 3t + 1 = 0
D = 9 - 4*2*1 = 1
t₁ = (- 3 - 1)/4 = - 1
t₂ = (- 3 + 1)/4 = - 1/2
1) tg2x = - 1
2x = arctg(-1) + πk, k ∈ Z
2x = - π/4 + πk, k ∈ Z
x₁ = - π/8 + πk/2, k ∈ Z
2) tg2x = - 1/2
2x = arctg(-1/2) + πn, n ∈ Z
x₂ = - (1/2)*arctg(1/2) + πn, n ∈ Z
3) sin(2x + 12π/7) = 2sin(x - π/7)
- sin2x = - 2sinx
2sinxcosx - 2sinx = 0
2sinx(cosx - 1) = 0
1) sinx = 0
x₁ = πk, k ∈ Z
2) cosx - 1 = 0
cosx = 1
x₂ = 2πn, n ∈ z
1) sin³x*cosx - cos³x*sinx = 1/4
Умножим обе части уравнения на 4
4*(sin³x*·cosx - cos³x*sinx) = 1
4*(sin²x*sinx*cosx-cos²x*cosx*sinx) = 1
4*sinx*cosx*(sin²x - cos²x) = 1
- 2*(2*sinx*cosx)*(cos²x - sin²x) = 1
- 2*sin2x*cos2x = 1
- sin4x = 1
sin4x= - 1
4x = - π/2 + 2πk, k∈Z
x = - π/8 + πk/2, k∈Z
2) 2cos²2x + 3*2*sin2xcos2x + 4sin²2x = 0
2cos²2x +6sin2xcos2x + 4sin²2x = 0
делим на cos²2x ≠ 0
4tg²2x + 6tg2x + 2 = 0
делим на 2
2tg²2x +3tg2x + 1 = 0
tg2x = t
2t² + 3t + 1 = 0
D = 9 - 4*2*1 = 1
t₁ = (- 3 - 1)/4 = - 1
t₂ = (- 3 + 1)/4 = - 1/2
1) tg2x = - 1
2x = arctg(-1) + πk, k ∈ Z
2x = - π/4 + πk, k ∈ Z
x₁ = - π/8 + πk/2, k ∈ Z
2) tg2x = - 1/2
2x = arctg(-1/2) + πn, n ∈ Z
x₂ = - (1/2)*arctg(1/2) + πn, n ∈ Z
3) sin(2x + 12π/7) = 2sin(x - π/7)
- sin2x = - 2sinx
2sinxcosx - 2sinx = 0
2sinx(cosx - 1) = 0
1) sinx = 0
x₁ = πk, k ∈ Z
2) cosx - 1 = 0
cosx = 1
x₂ = 2πn, n ∈ z
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Алгебра,
автор: chino25
Предмет: Математика,
автор: sasapu269
Предмет: Литература,
автор: Dinochka1999
Предмет: Математика,
автор: геля000056