Предмет: Геометрия,
автор: Аноним
Геометрия.Задание во вложении.
Приложения:
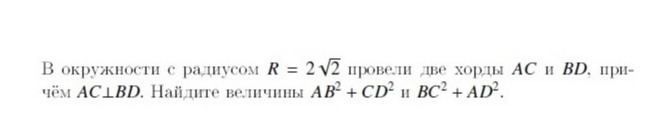
Andr1806:
Несколько не то.
Ответы
Автор ответа:
2
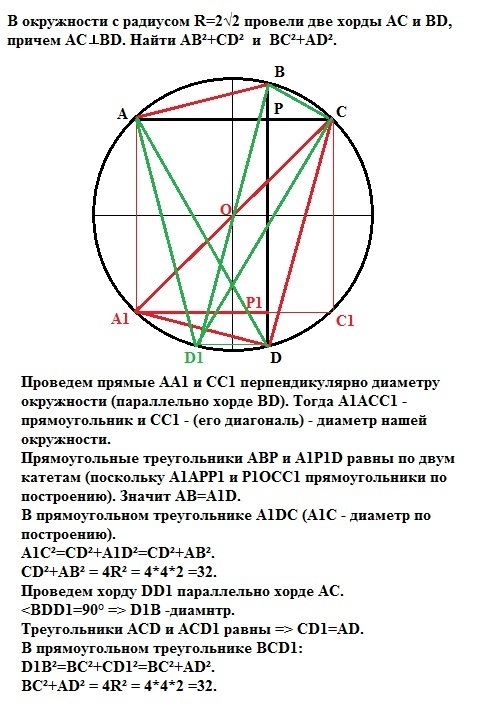
В окружности с радиусом R=2√2 провели две хорды АС и ВD, причем
АС⊥BD. Найти АВ²+СD² и ВC²+AD²
Решение.
Проведем прямые АА1 и СС1 перпендикулярно диаметру окружности (параллельно хорде BD). Тогда А1АСС1 - прямоугольник и СС1 - (его диагональ) - диаметр нашей окружности.
Прямоугольные треугольники АВР и А1P1D равны по двум катетам (поскольку А1АРР1 и Р1ОСС1 прямоугольники по построению).
Значит АВ=A1D.
В прямоугольном треугольнике А1DC (А1С - диаметр по построению).
А1С²=CD²+A1D²=CD²+AB².
CD²+AB² = 4R² = 4*4*2 =32.
Проведем хорду DD1 параллельно хорде АС.
<BDD1=90° => D1B -диаметр.
Треугольники ACD и ACD1 равны => CD1=AD.
В прямоугольном треугольнике BCD1:
D1B²=BC²+CD1²=BC²+AD².
BC²+AD² = 4R² = 4*4*2 =32.
Ответ: CD²+AB² = BC²+AD²= 32.
АС⊥BD. Найти АВ²+СD² и ВC²+AD²
Решение.
Проведем прямые АА1 и СС1 перпендикулярно диаметру окружности (параллельно хорде BD). Тогда А1АСС1 - прямоугольник и СС1 - (его диагональ) - диаметр нашей окружности.
Прямоугольные треугольники АВР и А1P1D равны по двум катетам (поскольку А1АРР1 и Р1ОСС1 прямоугольники по построению).
Значит АВ=A1D.
В прямоугольном треугольнике А1DC (А1С - диаметр по построению).
А1С²=CD²+A1D²=CD²+AB².
CD²+AB² = 4R² = 4*4*2 =32.
Проведем хорду DD1 параллельно хорде АС.
<BDD1=90° => D1B -диаметр.
Треугольники ACD и ACD1 равны => CD1=AD.
В прямоугольном треугольнике BCD1:
D1B²=BC²+CD1²=BC²+AD².
BC²+AD² = 4R² = 4*4*2 =32.
Ответ: CD²+AB² = BC²+AD²= 32.
Приложения:
Автор ответа:
1
Решение в приложении.
Приложения:

Похожие вопросы
Предмет: Русский язык,
автор: Аноним
Предмет: Математика,
автор: iliadenisovich2011
Предмет: Другие предметы,
автор: liza23alekseenko57
Предмет: Алгебра,
автор: alivinavina22