Question

Найдите площадь фигуры, ограниченную линиями. xy=6 и x+y-7=0. Только подробно.

Answer 1

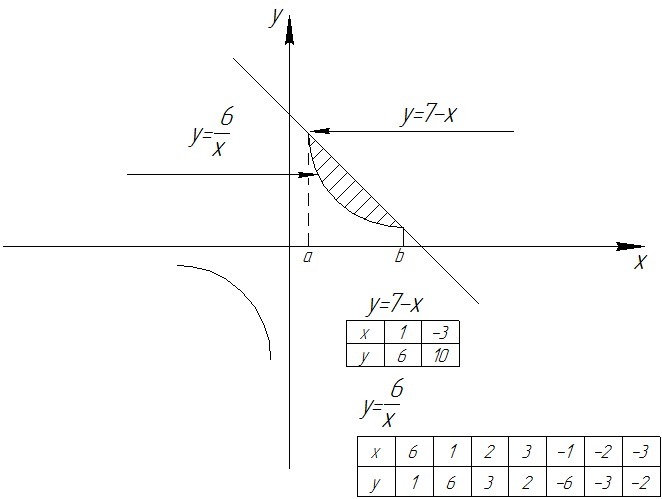
Графиком функции $y=7-x$ является прямая.

Графиком функции $y= \frac{6}{x}$ являются ветви гиперболы. 

Найдем абсциссы точек пересечения заданных линий:

$\left \{ {{y= \frac{6}{x} } \atop {y=7-x}} \right.\\ \frac{6}{x} =7-x\\-x^2+7x-6=0\\x_1=1\\x_2=6$

$x_1,x_2$- пределы интегрирования. (на рисунке изображены как "a" и "b".

$S= \int\limits^6_1 ({7-x- \frac{6}{x}) } \, dx= \int\limits^6_1 {7} \, dx - \int\limits^6_1 {x} \, dx- \int\limits^6_1{ \frac{6}{x} \, dx=7x\ |^6_1- \frac{x^2}{2}\ |^6_1-6ln|x|\ |^6_1$

$=(42-7)-(18-0,5)-6*ln|6|=17,5-6*ln|6|$≈7,4 (кв. ед.)