Question

16 задание математика егэ (100б)

Answer 1

a)

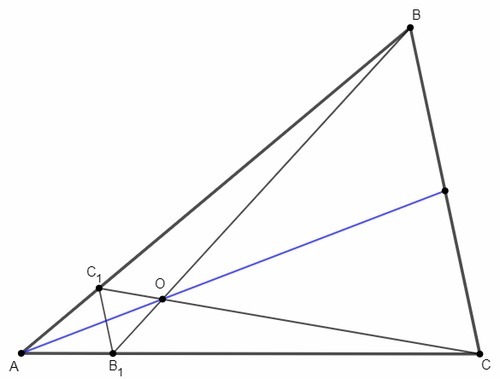
Прямые B1C1 и BC отсекают на сторонах AB и AC пропорциональные отрезки, начиная от вершины A, следовательно, по обратной теореме о пропорциональных отрезках, B1C1 параллельна BC.

AB1/B1C =AC1/C1B <=> AB1/AC1 =B1C/C1B => B1C1 || BC

B1C1BC - трапеция.

В трапеции точка пересечения продолжения боковых сторон, середины двух оснований и точка пересечения диагоналей лежат на одной прямой.

В трапеции B1C1BC прямая AO проходит через точку пересечения продолжения боковых сторон (A) и точку пересечения диагоналей (O), следовательно проходит через середину основания BC.

b)

△AC1B1~△ABC (по двум углам, углы при параллельных основаниях C1B1 и BC равны как соответственные)
AB1/B1C=1/4, AC=AB1+B1C
AC/AB1 =(AB1+B1C)/AB1 =1 +B1C/AB1 =5
k= AB1/AC =1/5 (коэффициент подобия)

Площади подобных треугольников относятся как квадрат коэффициента подобия.
S(△AC1B1)/S(△ABC) =1/25

Диагонали трапеции делят ее на два подобных треугольника (прилежащих основаниям) и два треугольника равной площади (прилежащих боковым сторонам).

△OB1C1~△OBC
k= B1C1/BC =AB1/AC =1/5 (△AC1B1~△ABC)

h1 - высота △OB1C1
h2 - высота △OBC
h - высота трапеции B1C1BC
h1/h2=1/5 => h= h1+h2 =6h1
S(△OB1C1)= B1C1*h1 /2
S(B1C1BC)= (B1C1+BC)*h/2 = 6B1C1*6h1 /2 =36 *B1C1*h1 /2
S(△OB1C1)/S(B1C1BC) =1/36

S(△AC1B1)=a
S(△OB1C1)=b
S(B1C1BC)=c
a/(a+c)=1/25 <=> a+c=25a <=> c=24a
b/c=1/36 <=> b=c/36
a+b =a +c/36 =a +24a/36 =5a/3
(a+b)/(a+c) = 5a/3 : 25a =1/15

Ответ: S(AB1OC1)/S(ABC) =1/15