Предмет: Алгебра,
автор: anna05141
Пожалуйста, решите уравнение:
Приложения:
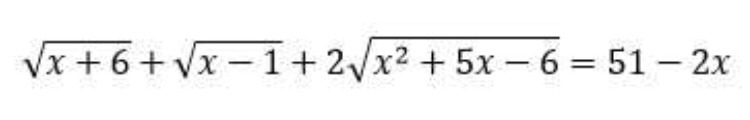
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Русский язык,
автор: o0oo0o00000
Предмет: Қазақ тiлi,
автор: ziroinsava
Предмет: Математика,
автор: 17537
Предмет: Математика,
автор: 00TheEnd00
Предмет: Математика,
автор: катя15151