Предмет: Алгебра,
автор: 34F
Помогите с интегралами
Приложения:
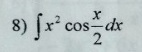
Ответы
Автор ответа:
0
Я решал последовательно, что непонятно, спрашивай
Этой формулой будем пользоваться





Этой формулой будем пользоваться
Приложения:

Похожие вопросы
Предмет: Биология,
автор: aitgwax11
Предмет: Литература,
автор: kukas39
Предмет: Химия,
автор: novikovdani4
Предмет: Математика,
автор: Irfan228