Question

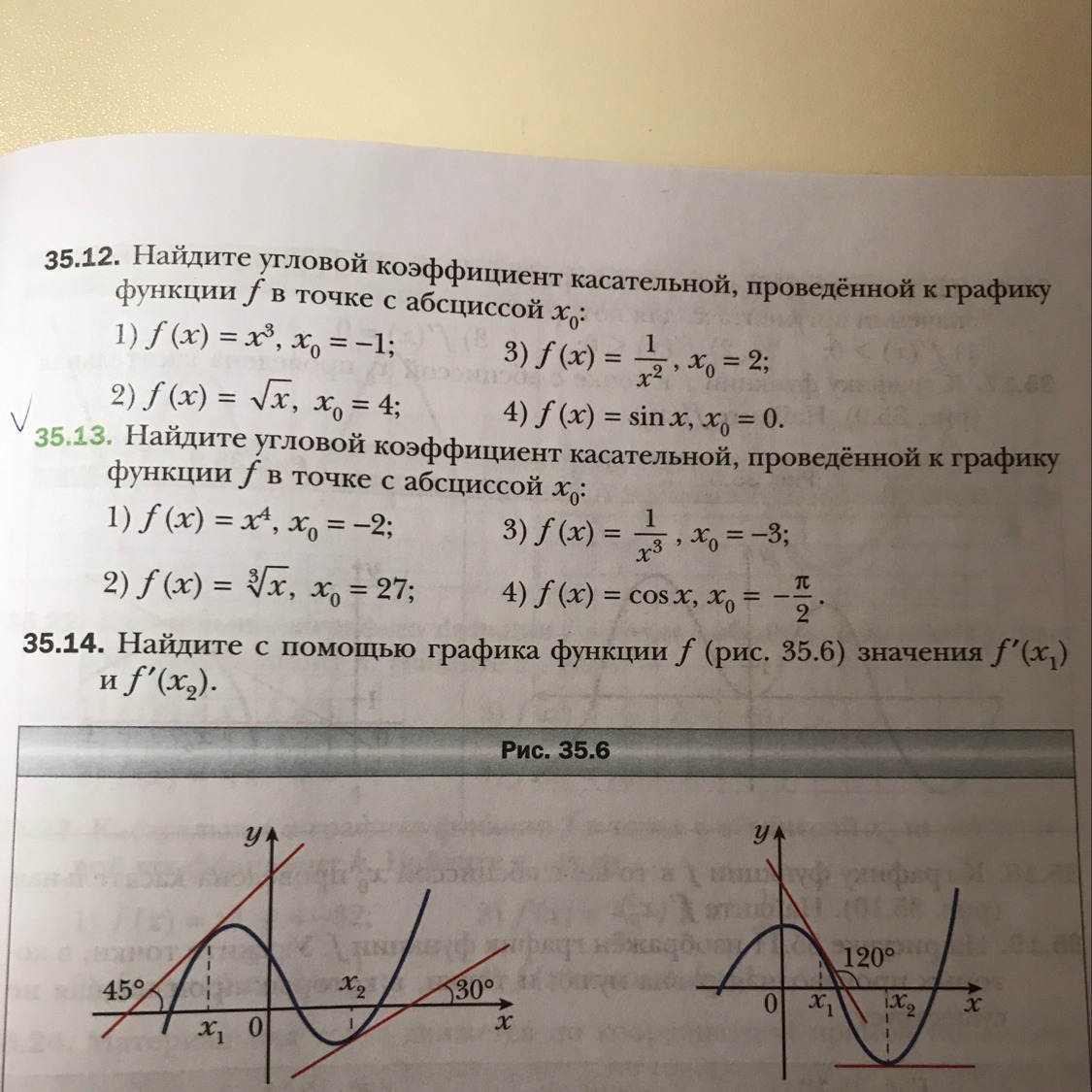
Очень срочно надо, начиная со 2 примера (упражнение 35.13)
!!!!!!! Плиииииз!!!!!

Answer 1

уравнение кассательной:$L(x)=f(x_0)+f'(x_0)*(x-x_0)\\\\ L(x)=k*x+b\\\\ k=f'(x_0)\\\\ b=f(x_0)-f'(x_0)*x_0$

$(2)\\ f(x)=\sqrt[3]{x}=x^{\frac{1}{3}},\ \ \ x_0=27\\\\ f'(x)=[x^{\frac{1}{3}}]'=\frac{1}{3}*x^{\frac{1}{3}-1}=\frac{1}{3}*x^{-\frac{2}{3}}=\frac{1}{3*\sqrt[3]{x^2}}\\\\ k=f'(x_0)=f'(27)=\frac{1}{3*\sqrt[3]{27^2}}=\frac{1}{3*\sqrt[3]{3^6}}=\frac{1}{3*3^2}=\frac{1}{3^3}=\frac{1}{27}$

$(3)\\ f(x)=\frac{1}{x^3}=x^{-3},\ \ \ x_0=-3\\\\ f'(x)=[x^{-3}]'=-3*x^{-3-1}=-3*x^{-4}=-3*\frac{1}{x^4}=-\frac{3}{x^4}\\\\ k=f'(x_0)=f'(-3)=-\frac{3}{(-3)^4}=-\frac{1}{3^3}=-\frac{1}{27}$

$(4)\\ f(x)=cos(x), \ \ \ x_0=-\frac{\pi}{2}\\\\ f'(x)=[cos(x)]'=-sin(x)\\\\ k=f'(x_0)=f'(-\frac{\pi}{2})=-sin(-\frac{\pi}{2})=sin(\frac{\pi}{2})=1$