Предмет: Математика,
автор: Ryunosukee
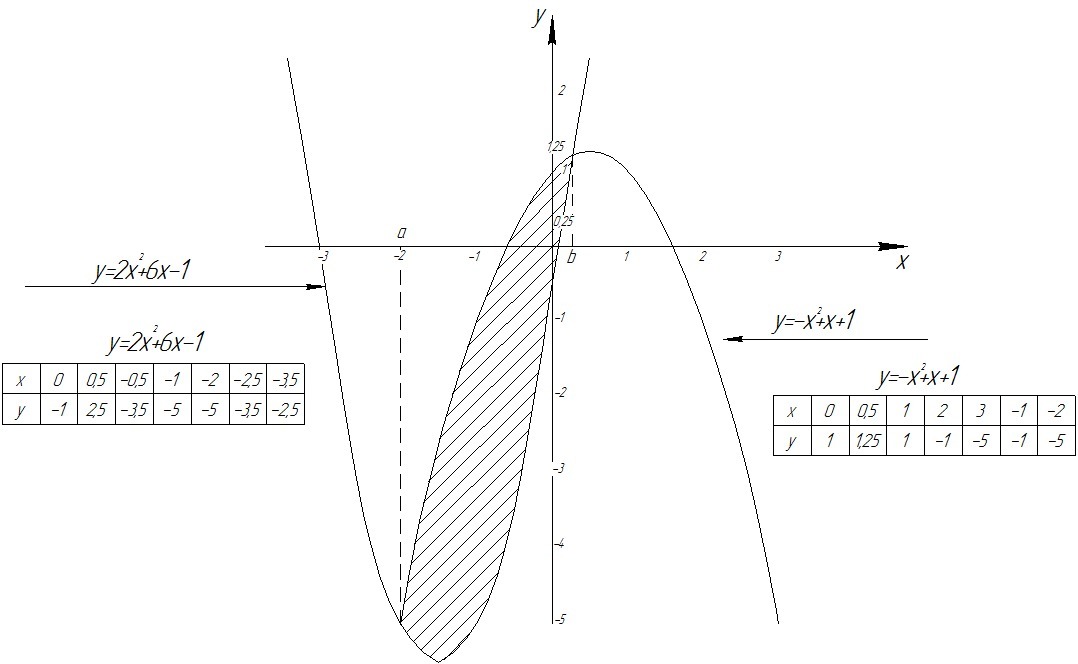
Вычислить площадь фигуры, ограниченной линиями:

Ответы
Автор ответа:
1
Автор ответа:
1
Найдем абсциссы точек пересечения заданных линий:

 - пределы интегрирования. (на рисунке изображены как "a" и "b".
- пределы интегрирования. (на рисунке изображены как "a" и "b".


Приложения:
Похожие вопросы
Предмет: Алгебра,
автор: gnomyhka
Предмет: География,
автор: rc0730184
Предмет: Математика,
автор: ashirovd2011
Предмет: Физика,
автор: deanclare