Предмет: Алгебра,
автор: Sayafarovskaya
докажите неравенство (номер 133)
Приложения:
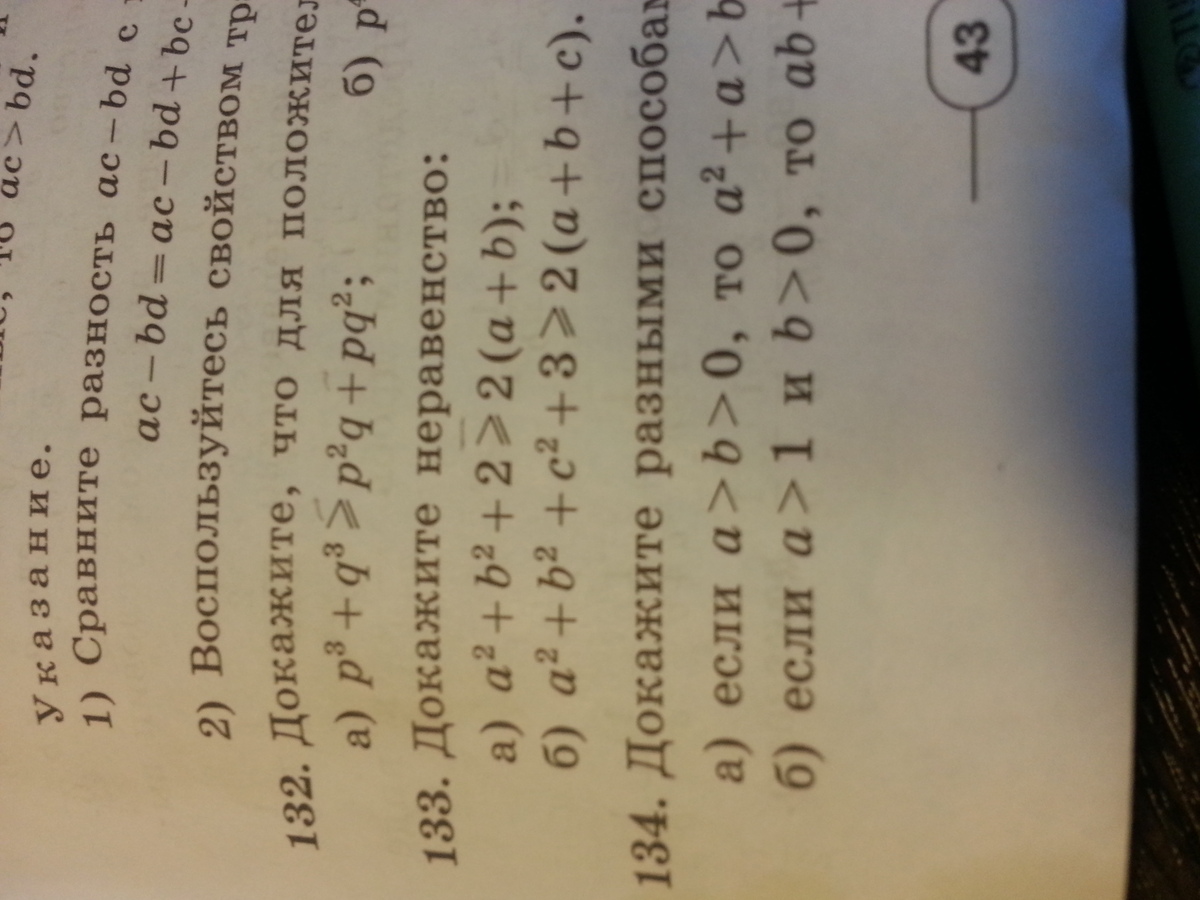
Ответы
Автор ответа:
0
Перекинем слагаемые в левую часть

Введем функцию , тогда
, тогда  , что доказывается построением графика.
, что доказывается построением графика.
Тогда выражение примет вид , в котором
, в котором  поэтому
поэтому  , что и требовалось доказать. В букве Б АБСОЛЮТНО то же самое, только функции три.
, что и требовалось доказать. В букве Б АБСОЛЮТНО то же самое, только функции три.
Введем функцию
Тогда выражение примет вид
Похожие вопросы
Предмет: Алгебра,
автор: Аноним
Предмет: Математика,
автор: denismnsunkry
Предмет: Русский язык,
автор: bdfy1708
Предмет: Алгебра,
автор: инюлька
Предмет: Алгебра,
автор: Grafomano4ka