Предмет: Алгебра,
автор: ниka3572
y=-x^2-8x+3 исследуйте функцию пжжжжжжж, срочно!!!!
Ответы
Автор ответа:
1
План исследование функции (9 класс)
1.Определить вид функции, если возможно (указать её название и название графика, если определили вид).
Функция y=-x^2-8x+3 квадратичная. Её график - парабола ветвями вниз.
2. Найти область определения функции (множество значений аргумента х, на котором данная функция определена): D(y) ∈ (-∞; +∞).
3. Найти область значения функции (множество значений функции у):
Находим вершину параболы.
Хо = -в/2а = -(-8)/(2*(-1)) = -4.
Уо = -4²-8*(-4)+3 = -16+32+3 = 19.
E(y) ∈ (-∞; 19).
4. Найти нули функции (точки пресечения с осью х) если возможно, для чего приравнять нулю у=0.
-x^2-8x+3 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-8)^2-4*(-1)*3=64-4*(-1)*3=64-(-4)*3=64-(-4*3)=64-(-12)=64+12=76;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√76-(-8))/(2*(-1))=(√76+8)/(2*(-1))=(√76+8)/(-2)=-(√76+8)/2=-(√76/2+8/2)=-(√76/2+4) = (-√19)-4 ≈ -8.358899;x_2=(-√76-(-8))/(2*(-1))=(-√76+8)/(2*(-1))=(-√76+8)/(-2)=-(-√76+8)/2=-(-√76/2+8/2)=-(-√76/2+4)=(√19)-4 ≈ 0.3588989.
5. Определить, при каких значениях аргумента х значения функции у>0, при каких значениях аргумента у <0.
у>0 при х ∈ (-∞; ((-√19)-4),
y>0 при х ∈ (((√19)-4); +∞).
6. Выяснить, является ли функция четной (симметричной относительно оси ординат) или нечетной (симметричной относительно начала координат).
Функция являентся ни четной, ни нечетной.
7. Построить таблицу значений данной функции.
х = -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1
у = -17 -6 3 10 15 18 19 18 15 10 3 -6.
8. Определить, является ли функция возрастающей (убывающей) или указать промежутки возрастания (убывания).
Функция возрастает при х ∈ (-∞; -4),
убывает при х ∈ (-4; +∞).
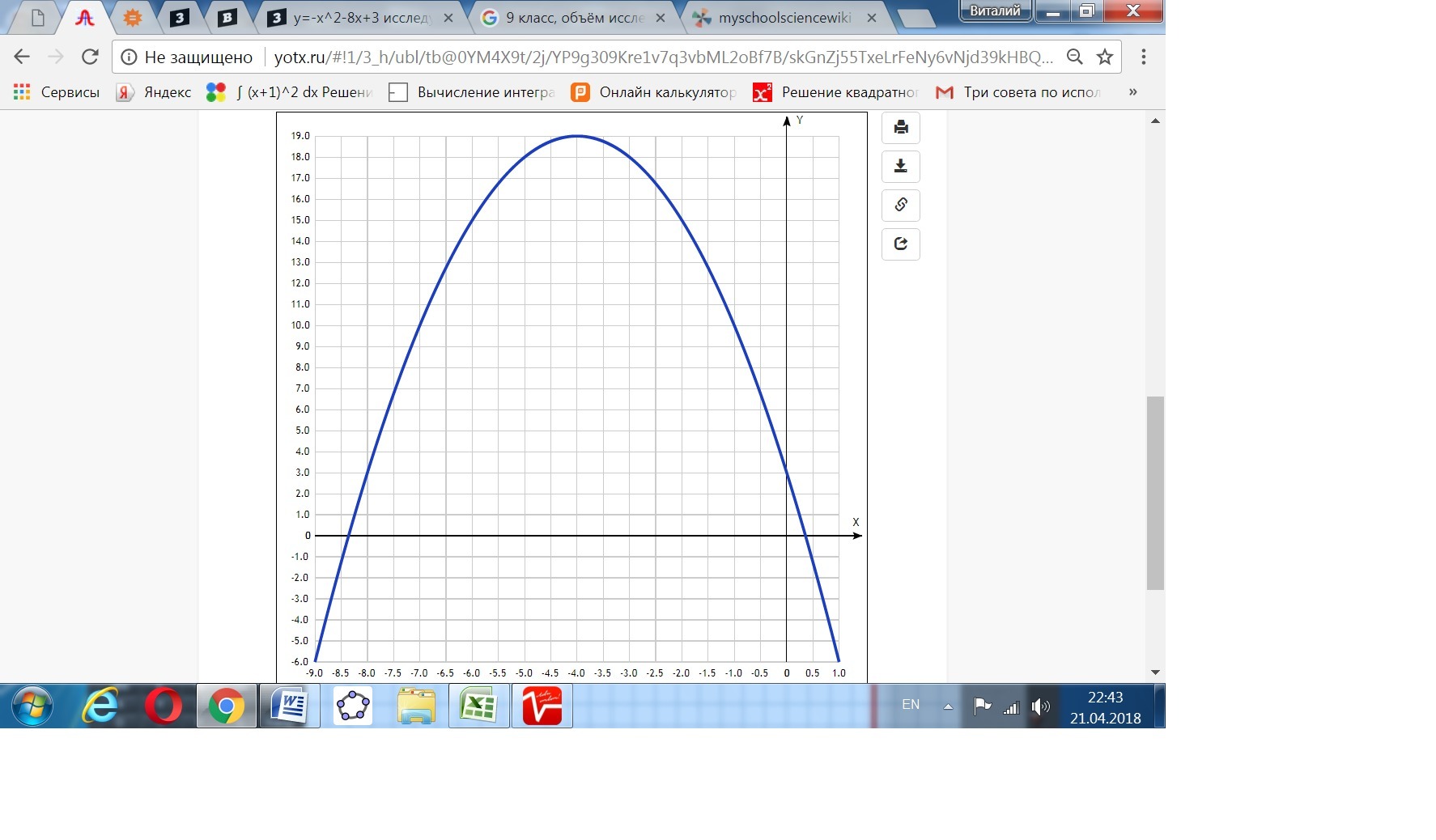
9. Начертить график, отметив в координатной плоскости точки, координаты которых соответствуют парам (х,у), полученным в таблице, и соединив их плавной (прямой) линией.
1.Определить вид функции, если возможно (указать её название и название графика, если определили вид).
Функция y=-x^2-8x+3 квадратичная. Её график - парабола ветвями вниз.
2. Найти область определения функции (множество значений аргумента х, на котором данная функция определена): D(y) ∈ (-∞; +∞).
3. Найти область значения функции (множество значений функции у):
Находим вершину параболы.
Хо = -в/2а = -(-8)/(2*(-1)) = -4.
Уо = -4²-8*(-4)+3 = -16+32+3 = 19.
E(y) ∈ (-∞; 19).
4. Найти нули функции (точки пресечения с осью х) если возможно, для чего приравнять нулю у=0.
-x^2-8x+3 = 0.
Квадратное уравнение, решаем относительно x: Ищем дискриминант:
D=(-8)^2-4*(-1)*3=64-4*(-1)*3=64-(-4)*3=64-(-4*3)=64-(-12)=64+12=76;Дискриминант больше 0, уравнение имеет 2 корня:
x_1=(√76-(-8))/(2*(-1))=(√76+8)/(2*(-1))=(√76+8)/(-2)=-(√76+8)/2=-(√76/2+8/2)=-(√76/2+4) = (-√19)-4 ≈ -8.358899;x_2=(-√76-(-8))/(2*(-1))=(-√76+8)/(2*(-1))=(-√76+8)/(-2)=-(-√76+8)/2=-(-√76/2+8/2)=-(-√76/2+4)=(√19)-4 ≈ 0.3588989.
5. Определить, при каких значениях аргумента х значения функции у>0, при каких значениях аргумента у <0.
у>0 при х ∈ (-∞; ((-√19)-4),
y>0 при х ∈ (((√19)-4); +∞).
6. Выяснить, является ли функция четной (симметричной относительно оси ординат) или нечетной (симметричной относительно начала координат).
Функция являентся ни четной, ни нечетной.
7. Построить таблицу значений данной функции.
х = -10 -9 -8 -7 -6 -5 -4 -3 -2 -1 0 1
у = -17 -6 3 10 15 18 19 18 15 10 3 -6.
8. Определить, является ли функция возрастающей (убывающей) или указать промежутки возрастания (убывания).
Функция возрастает при х ∈ (-∞; -4),
убывает при х ∈ (-4; +∞).
9. Начертить график, отметив в координатной плоскости точки, координаты которых соответствуют парам (х,у), полученным в таблице, и соединив их плавной (прямой) линией.
Приложения:
Похожие вопросы
Предмет: Английский язык,
автор: yarikgraw
Предмет: Русский язык,
автор: nikvera
Предмет: Алгебра,
автор: aaulymgabidolla659
Предмет: Физика,
автор: Frelm