Предмет: Алгебра,
автор: Гуля551
ПОМОГИТЕ ПОЖАЛУЙСТА!!!!
Приложения:
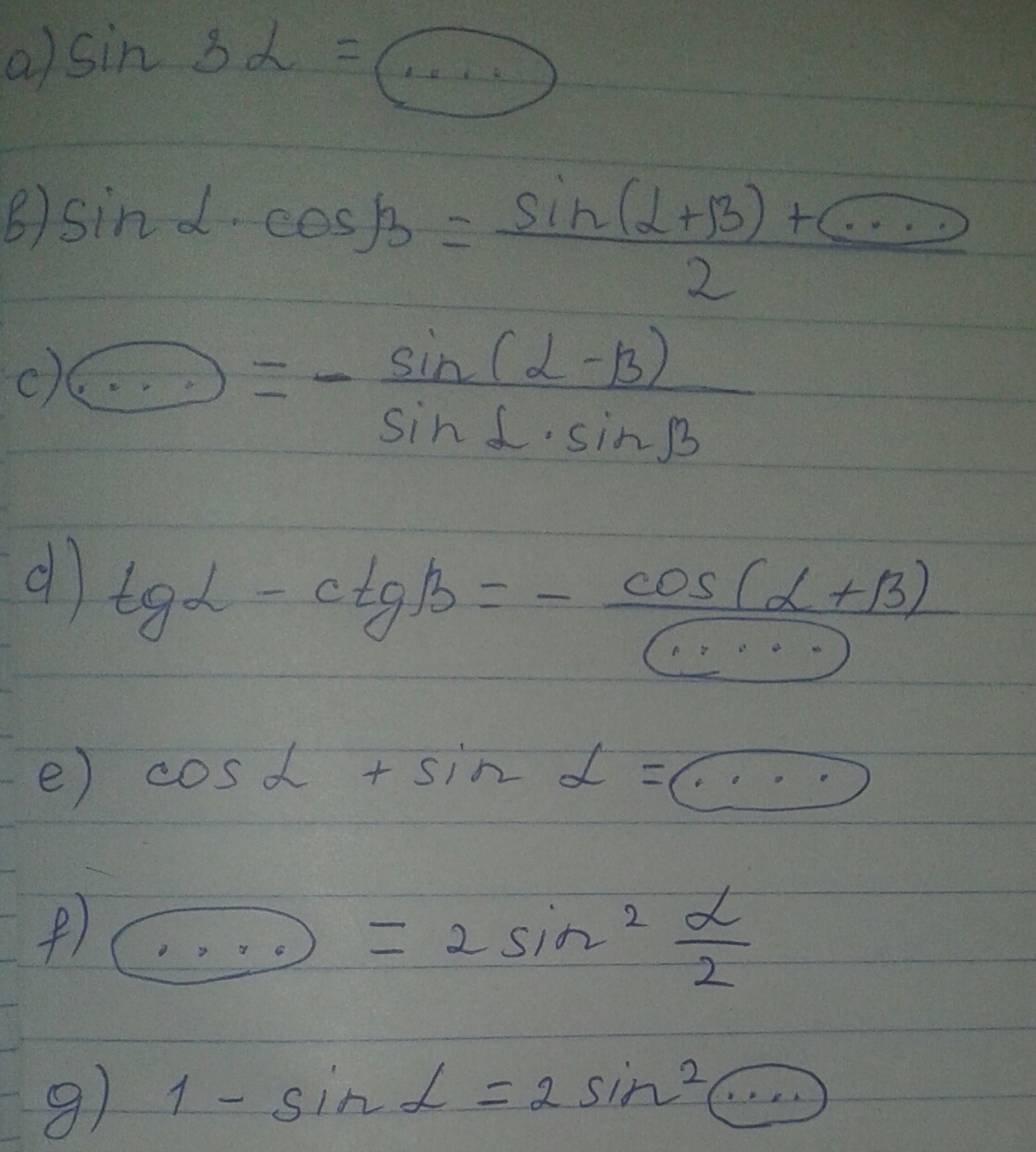
Ответы
Автор ответа:
1
task/28751900
-------------------
a) sin3α =... || sinα(3-4sin²α)
sin3α =sin(α +2α) =sinα*cos2α +cosα*sin2α =
sinα*(cos²α - sin²α) +cosα*2sinα*cosα =sinα(3cos²α -sin²α)=sinα(3-4sin²α).
-------------------
b) sinα*cosβ= ( sin(α+β) + ... ) /2 || sin(α - β)
2sinα*cosβ - sin(α+β) =2sinα*cosβ - (sinα*cosβ+cosα*sinβ) =
sinα*cosβ - cosα*sinβ =sin(α - β ).
-------------------
c) ... = - sin(α-β) / sinα*sinβ || ctgα - ctgβ
- sin(α-β) / sinα*sinβ = - (sinα*cosβ - cosα*sinβ) / sinα*sinβ =
cosα*sinβ /sinα*sinβ - sinα*cosβ / sinα*sinβ = ctgα - ctgβ .
-------------------
d) tgα - ctgβ = - cos(α+β) / ... || cosα *sinβ
- cos(α+β) / (tgα -ctgβ) = cos(α+β) / ( cosβ / sinβ - sinα / cosα) =
cos(α+β)*cosα*sinβ / (cosα*cosβ-sinα*sinβ)=cos(α+β) *cosα*sinβ /cos(α+β) = cosα *sinβ .
-------------------
e) cosα +sinα = ... || √2cos(α -π/4).
cosα +sinα =cosα +cos(π/2 - α) =2cos(α +π/2 - α)/2 * cos(α -(π/2 - α )) /2=
2cos(π/4 ) * cos(α -π/4) =√2cos(α -π/4).
или
cosα +sinα =√2( 1/√2)*cosα + (1/√2)*sinα ) =
√2( cos(π/4)*cosα + sin(π/4)*sinα) ) =√2cos(x - π/4) .
-------------------
f) ... = 2sin²(α/2) || 1 - cosα .
2sin²(α/2) =sin²(α/2) + sin²(α/2) = 1 - cos²(α/2) + sin²(α/2) =
1 -( cos²(α/2) - sin²(α/2) ) = 1 cos(2*(α/2) ) = 1 - cosα .
-------------------
g) 1- sinα =2sin² ... || (π/4 -α/2) .
1- sinα =1 - cos(π/2 -α) =1-cos2(π/4-α/2) =1-(cos²(π/4 -α/2)-sin²(π/4-α/2) ) = (1- cos²(π/4 -α/2) )+sin²(π/4-α/2) =sin²(π/4-α/2) +sin²(π/4-α/2) =
2sin²(π/4-α/2) .
* * * * * * * * все можно было написать сразу * * * * * * * *
Удачи !
-------------------
a) sin3α =... || sinα(3-4sin²α)
sin3α =sin(α +2α) =sinα*cos2α +cosα*sin2α =
sinα*(cos²α - sin²α) +cosα*2sinα*cosα =sinα(3cos²α -sin²α)=sinα(3-4sin²α).
-------------------
b) sinα*cosβ= ( sin(α+β) + ... ) /2 || sin(α - β)
2sinα*cosβ - sin(α+β) =2sinα*cosβ - (sinα*cosβ+cosα*sinβ) =
sinα*cosβ - cosα*sinβ =sin(α - β ).
-------------------
c) ... = - sin(α-β) / sinα*sinβ || ctgα - ctgβ
- sin(α-β) / sinα*sinβ = - (sinα*cosβ - cosα*sinβ) / sinα*sinβ =
cosα*sinβ /sinα*sinβ - sinα*cosβ / sinα*sinβ = ctgα - ctgβ .
-------------------
d) tgα - ctgβ = - cos(α+β) / ... || cosα *sinβ
- cos(α+β) / (tgα -ctgβ) = cos(α+β) / ( cosβ / sinβ - sinα / cosα) =
cos(α+β)*cosα*sinβ / (cosα*cosβ-sinα*sinβ)=cos(α+β) *cosα*sinβ /cos(α+β) = cosα *sinβ .
-------------------
e) cosα +sinα = ... || √2cos(α -π/4).
cosα +sinα =cosα +cos(π/2 - α) =2cos(α +π/2 - α)/2 * cos(α -(π/2 - α )) /2=
2cos(π/4 ) * cos(α -π/4) =√2cos(α -π/4).
или
cosα +sinα =√2( 1/√2)*cosα + (1/√2)*sinα ) =
√2( cos(π/4)*cosα + sin(π/4)*sinα) ) =√2cos(x - π/4) .
-------------------
f) ... = 2sin²(α/2) || 1 - cosα .
2sin²(α/2) =sin²(α/2) + sin²(α/2) = 1 - cos²(α/2) + sin²(α/2) =
1 -( cos²(α/2) - sin²(α/2) ) = 1 cos(2*(α/2) ) = 1 - cosα .
-------------------
g) 1- sinα =2sin² ... || (π/4 -α/2) .
1- sinα =1 - cos(π/2 -α) =1-cos2(π/4-α/2) =1-(cos²(π/4 -α/2)-sin²(π/4-α/2) ) = (1- cos²(π/4 -α/2) )+sin²(π/4-α/2) =sin²(π/4-α/2) +sin²(π/4-α/2) =
2sin²(π/4-α/2) .
* * * * * * * * все можно было написать сразу * * * * * * * *
Удачи !
Гуля551:
Помогите с алгеброй пожалуйста. Я задала вопрос
Похожие вопросы
Предмет: Математика,
автор: anastasijakanp15u85
Предмет: Математика,
автор: beslanadzinov
Предмет: Математика,
автор: tujcievamavluda9
Предмет: Математика,
автор: olesyapavlova1