Question

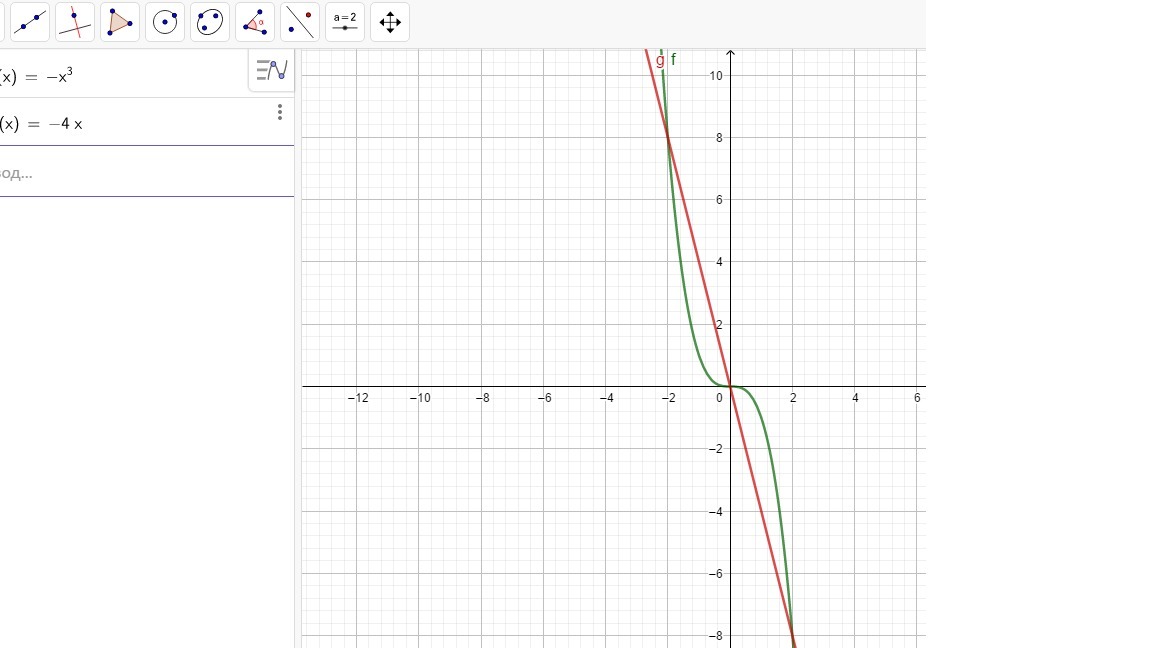
Вычислить площадь плоской области , ограниченной данными линиями. Построить область D.
$y=-x^3, y=-4x$

Answer 1

Образуются две симметричные равные по площади фигуры
Найдем площадь одной из них, после чего удвоим результат
$\int\limits^2_0 ({ -x^{3}+4x} )\ dx = - \frac{x^{4}}{4} +2x^{2} = -4+8=4$
4*2=8
Ответ: 8