Предмет: Алгебра,
автор: настюшечка97
Помогите решить задание во вложениях
Приложения:
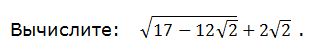
Ответы
Автор ответа:
0
"как ""нетрудно"" заметить", подкоренное выражение ---это полный квадрат...
"квадрат первого+квадрат второго" = 17
"удвоенное произведение первого на второй" = 12V2 = 2 * (2V2) * 3
второй член формулы квадрат разности под корнем лучше подбирать, равным слагаемому вне корня (чтобы потом они уничтожились...)
итак, второй член формулы --- 2V2, тогда первый очевидно 3...
проверяем (3)^2 - 2*3*2V2 + (2V2)^2 = 9 - 12V2 + 8 = 17 - 12V2...
тогда из первого корня извлечется: |3 - 2V2|
напомню, что V(a^2) = |a|
и теперь нужно оценить знак выражения под модулем...
т.к. 3^2 > (2V2)^2...
значит 3 > 2V2...
следовательно, по определению модуля |3 - 2V2| = 3 - 2V2
в итоге получим: 3 - 2V2 + 2V2 = 3
"квадрат первого+квадрат второго" = 17
"удвоенное произведение первого на второй" = 12V2 = 2 * (2V2) * 3
второй член формулы квадрат разности под корнем лучше подбирать, равным слагаемому вне корня (чтобы потом они уничтожились...)
итак, второй член формулы --- 2V2, тогда первый очевидно 3...
проверяем (3)^2 - 2*3*2V2 + (2V2)^2 = 9 - 12V2 + 8 = 17 - 12V2...
тогда из первого корня извлечется: |3 - 2V2|
напомню, что V(a^2) = |a|
и теперь нужно оценить знак выражения под модулем...
т.к. 3^2 > (2V2)^2...
значит 3 > 2V2...
следовательно, по определению модуля |3 - 2V2| = 3 - 2V2
в итоге получим: 3 - 2V2 + 2V2 = 3
Похожие вопросы
Предмет: Математика,
автор: ilasovaasal
Предмет: Химия,
автор: Lolll234
Предмет: Алгебра,
автор: Vadim7634
Предмет: Геометрия,
автор: crepe