Question

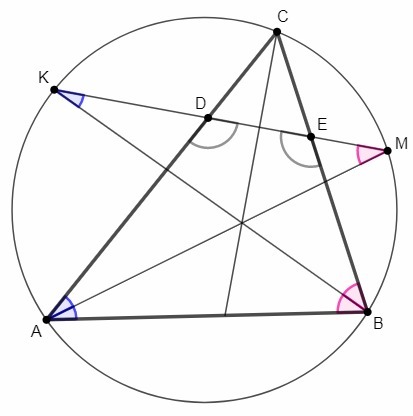
биссектрисы двух углов треугольника пересекают описанную вокруг него окружность в точках M и K. Докажите что отрезок MK перпендикулярен биссектрисе третьего угла

Answer 1

∠DAM=∠BAM (AM - биссектиса ∠A).
∠BAM=∠K (вписанные углы, опирающиеся на ∪BM).
∠DAM=∠K

Аналогично ∠EBK=∠M.

△ADM~△KEB (по двум углам), ∠ADM=∠KEB.

∠CDE=∠CED (смежные с равными), △DCE - равнобедренный, биссектриса к основанию является высотой, т.е. перпендикулярна DE (MK).