Question

Помогите, пожалуйста, решить задачу по геометрии:
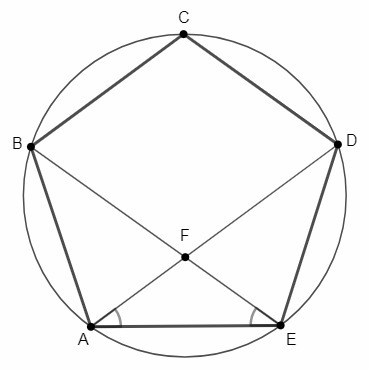
Пятиугольник ABCDE, все стороны которого равны, вписан в окружность. Найдите угол между двумя диагоналями, которые пересекаются во внутренних точках.

Answer 1

Равные хорды стягивают равные дуги. Пять равных хорд, являющихся сторонами пентагона, делят окружность на пять равных дуг.
∪AB=∪BC=∪CD=∪DE=∪AE =360°/5=72°

AD, BE - диагонали пентагона, пересекающиеся в точке F.

Вписанный угол равен половине угловой меры дуги, на которую опирается.
∠AEB=∪AB/2 =72°/2
∠DAE=∪DE/2 =72°/2

Сумма углов треугольника 180°.
△AFE: ∠AFE= 180°-∠AEB-∠DAE =180°-72° =108°

Мерой угла между пересекающимися прямыми считается мера меньшего из образованных углов.
∠AFB=180°-∠AFE =72°