Предмет: Алгебра,
автор: iojhhjkl
Очень нужно это задание!!
Найдите площадь фигуры, ограниченной линии
1. y= 6x^2 -2x+6, x=2, x=3, OX
2. y= 2-x^2, y=x^2+2x-2
Ответы
Автор ответа:
1
Первое кажется будет так
Приложения:
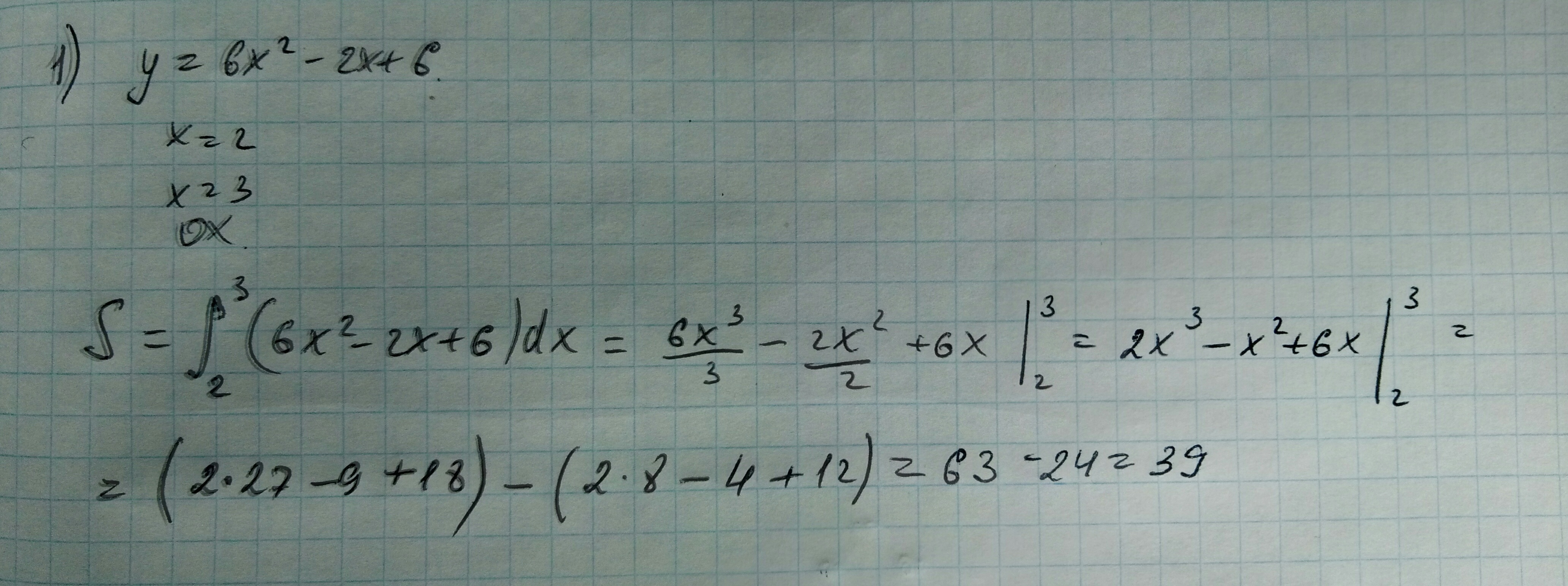
Автор ответа:
1
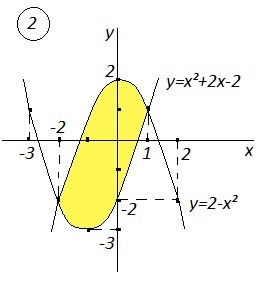
2) Точки пересечения парабол y=2-x² и y=x²+2x-2 :
2-х²=х²+2х-2 , 2х²+2х-4=0 , х²+х-2=0 , x₁=-2 , x₂=1 .
Смотри рисунок.

2-х²=х²+2х-2 , 2х²+2х-4=0 , х²+х-2=0 , x₁=-2 , x₂=1 .
Смотри рисунок.
Приложения:
Похожие вопросы
Предмет: История,
автор: tayusamu
Предмет: Литература,
автор: glazkovadiana78
Предмет: Математика,
автор: dorawix99
Предмет: Физика,
автор: данияр0001
Предмет: Алгебра,
автор: vladkrav01