Question

Найдите объем конуса, если его осевое сечение - треугольник с периметром P и тупым углом α .

Answer 1

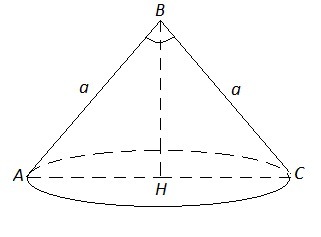
Сечение - ΔАВС - равнобедренный Δ ,  периметр  Р=2·АВ+АС=2а+АС.
∠АВС=α  ⇒  ∠АВН=α/2
Из ΔАВН:  АН=a·sinα/2  ,  BH=a·cosα/2 .
P=2a+2·AH=2a+2a·sinα/2=2a·(1+sinα/2)   ⇒   a=P/(2(1+sinα/2)) , 
AH=(Psinα/2)/(2(1+sinα/2))
BH=(Pcosα/2)/(2(1+sinα/2))

$V= \frac{1}{3}\pi R^2\cdot H=\frac{1}{3}\cdot \pi \cdot AH^2\cdot BH=\frac{\pi }{3}\cdot (a\cdot sin\frac{ \alpha }{2})^2\cdot (a\cdot cos\frac{ \alpha }{2})=\\\\= \frac{\pi }{3}\cdot \frac{P^2\cdot sin^2\frac{ \alpha }{2}}{4(1+sin\frac{ \alpha }{2})^2}\cdot \frac{P\cdot cos\frac{ \alpha }{2}}{2(1+sin\frac{ \alpha }{2})}=\frac{\pi }{3}\cdot \frac{P^3\cdot sin^2\frac{ \alpha }{2}\cdot cos\frac{ \alpha }{2}}{8(1+sin\frac{\alpha }{2})^3}$