Question

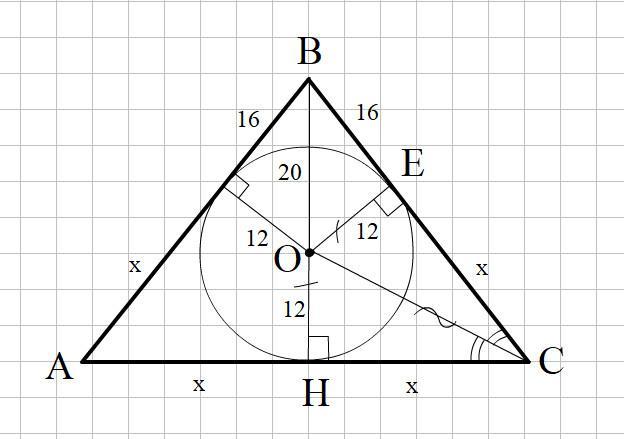
Радиус окружности, вписанной в равнобедренный треугольник АВС с основанием АС, равен 12 см, а расстояние от центра этой окружности до вершины В - 20 см. Найдите периметр данного треугольника.

Answer 1

Ответ:

Р = 128 см

Объяснение:

Смотри прикреплённый рисунок: ОВ = 20 см; ОЕ=ОН = r = 12 cм.

Центр О окружности, вписанной в треугольник, находится на пересечении биссектрис.

Из ΔОВЕ по теореме Пифагора найдём

ВЕ = √(ОВ² - ОЕ²) = √ (20² - 12²) = 16 (см)

ΔСНО = ΔСЕО  Треугольник прямоугольный: гипотенуза ВО - общая, и катеты ОЕ = ОН = 12 см  являются  радиусами вписанной окружности.

Тогда равны и отрезки СЕ = СН = х, а основание АС = 2х в силу симметрии треугольника относительно высоты (медианы) ВН.

Тогда  АВ = ВС = 16 + х

Периметр ΔАВС    Р =2 (16 + х) + 2х = 32 + 4х

Полупериметр ΔАВС    р = 16 + 2х

р - АВ = р - ВС = х;   р - АС = 16

По формуле Герона площадь ΔАВС равна

S = √(р (р - АВ)(р - ВС)(р - АС)) = √((16 + 2х) · х · х · 16) = √ (256х² + 32х³)

Высота ВН треугольника АВС равна ВН = ОВ + ВН = 20 + 12 = 32 (см)

Основание АС = 2х

Площадь ΔАВС равна

S = 0.5 AC · BH = 0.5 · 2x · 32 = 32x

Тогда 32х = √ (256х² + 32х³)

Возведём в квадрат обе части равенства

32²х² = 256х² + 32х³

32х² = 8х² + х³

х³ - 24х² = 0

х²(х - 24) = 0

х = 0 не подходит

х = 24 (см) - половина основания

Тогда Р = 32 + 4х = 32 + 4 · 24 = 128 (см)