Предмет: Математика,
автор: reyzi77
Решить б и г.
!!!Методом подстановки!!!
Приложения:
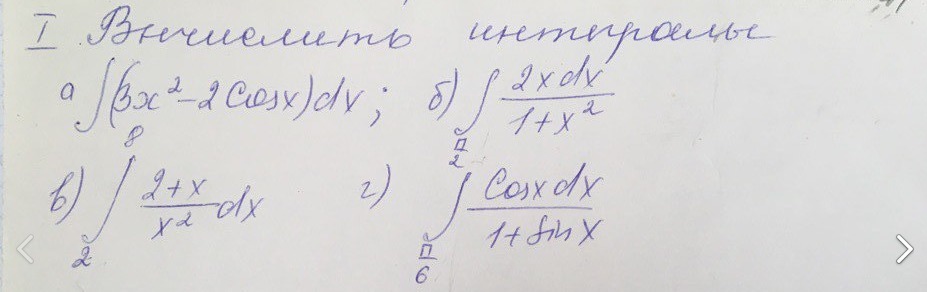
Ответы
Автор ответа:
1
b)

g)

g)
Похожие вопросы
Предмет: Математика,
автор: Madhacar
Предмет: Химия,
автор: Аноним
Предмет: Английский язык,
автор: Megarodon
Предмет: Алгебра,
автор: Lev0607
Предмет: Математика,
автор: kat1984sw