Предмет: Геометрия,
автор: Аноним
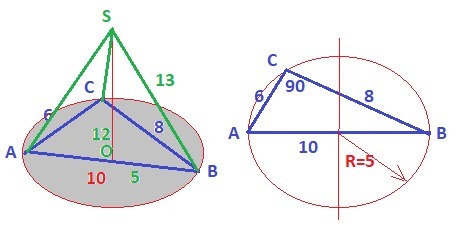
1.) расстояние от точки s до каждой вершины прямоугольного треугольника АВС ( угол С = 90 градусов ) равна : 13 см . Найдите расстояние от точки S до плоскости треугольника , если АС=6см , ВС=8см .
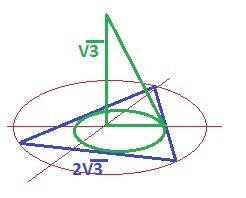
2.) Точка S равноудалена от каждой стороны правильного треугольника АВС , которая равна 2 корня из 3 . Найдите расстояние от точки S до стороны АВ , если расстояние от точки S до плоскости АВС равно корень из 3 см .
Ответы
Автор ответа:
1
РЕШЕНИЕ
1.
Рисунок к задаче в приложении.
Вычисляем гипотенузу АВ по т. Пифагора (3:4:5)
АВ = 10 ("в уме")
Прямоугольный треугольник опирается на диаметр описанной окружности
АВ = 10 - диаметр
AO = R = 5.
Высоту OS - расстояние до точки S также по т. Пифагора
OS = √(13²-5²) = √(169-25) = √144 = 12 - расстояние - ОТВЕТ
2.
Рисунок у задаче в приложении.
Радиус вписанной окружности в правильный треугольник по формуле
r = a/2√3 = 1 - радиус и катет
Находим гипотенузу - расстояние до стороны
b² = (√3)² + 1² = 4
b = √4 = 2 - расстояние - ОТВЕТ
1.
Рисунок к задаче в приложении.
Вычисляем гипотенузу АВ по т. Пифагора (3:4:5)
АВ = 10 ("в уме")
Прямоугольный треугольник опирается на диаметр описанной окружности
АВ = 10 - диаметр
AO = R = 5.
Высоту OS - расстояние до точки S также по т. Пифагора
OS = √(13²-5²) = √(169-25) = √144 = 12 - расстояние - ОТВЕТ
2.
Рисунок у задаче в приложении.
Радиус вписанной окружности в правильный треугольник по формуле
r = a/2√3 = 1 - радиус и катет
Находим гипотенузу - расстояние до стороны
b² = (√3)² + 1² = 4
b = √4 = 2 - расстояние - ОТВЕТ
Приложения:
Похожие вопросы
Предмет: История,
автор: sulkovskijmaksim0
Предмет: Математика,
автор: karinautebaeva0
Предмет: Алгебра,
автор: Kefr
Предмет: Математика,
автор: NGAYYYY