Предмет: Алгебра,
автор: ПрофиЗнания
Определить область сходимости функций рядов.
Приложения:
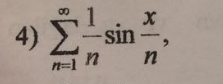
IUV:
рад сходится при х - любом
Ответы
Автор ответа:
0
наш ряд ограничен сверху рядом типа 1/n^2
1/n*sin(x/n) < 1/n*(x/n) = x/n^2
значит наш ряд тоже сходится, причем R= беск
1/n*sin(x/n) < 1/n*(x/n) = x/n^2
значит наш ряд тоже сходится, причем R= беск
можно по подробнее?
при любом значении переменной |sin(x)| <= |x|
это значит что |1/n*sin(x/n)| <= |1/n*(x/n)|= |x/n^2|
исходный ряд ограничен сверху сходящимся рядом
сумма ряда x/n^2 равна (х*пи^2)/6
значит сумма нашего ряда меньше (х*пи^2)/6
значит наш ряд сходится и радиус сходимости - бесконечность
это значит что |1/n*sin(x/n)| <= |1/n*(x/n)|= |x/n^2|
исходный ряд ограничен сверху сходящимся рядом
сумма ряда x/n^2 равна (х*пи^2)/6
значит сумма нашего ряда меньше (х*пи^2)/6
значит наш ряд сходится и радиус сходимости - бесконечность
Решите остальные
Похожие вопросы
Предмет: Литература,
автор: veronikatv33
Предмет: Литература,
автор: liudmilasuhoruk
Предмет: Биология,
автор: Darua1257
Предмет: Математика,
автор: martirosyankar
Предмет: Математика,
автор: мад1