Предмет: Алгебра,
автор: Аноним
Помогите решить логарифмы, знатоки. Заранее спасибо!
Приложения:
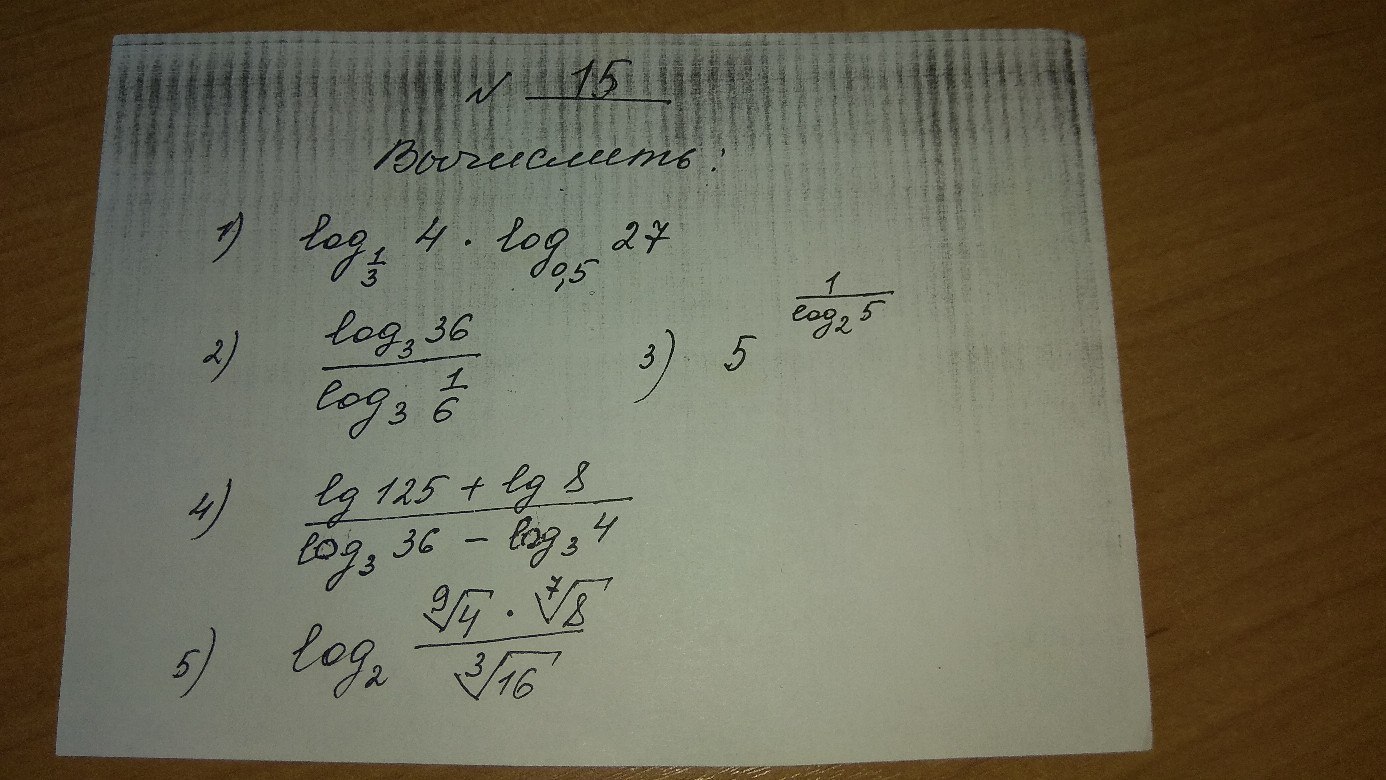
Ответы
Автор ответа:
1
Похожие вопросы
Предмет: Математика,
автор: Khocolatka228
Предмет: Алгебра,
автор: glebgersvild
Предмет: Русский язык,
автор: nurai263
Предмет: Математика,
автор: Алина08934
Предмет: Математика,
автор: vasilchansky