Предмет: Геометрия,
автор: chex113
БиссИз вершины A треугольника ABC опущены перпендикуляр AX на биссектрису угла B и перпендикуляр AY на биссектрису внешнего угла C. Чему равна длина отрезка XY, если AB=5, AC=11, BC=12?
Ответы
Автор ответа:
47
Даны длины сторон треугольника AB=5, AC=11, BC=12.
Из вершины A треугольника ABC опущены перпендикуляр AX на биссектрису угла B и перпендикуляр AY на биссектрису внешнего угла C.
Найти длину отрезка ХУ.
Данную задачу можно решить двумя способами:
1) геометрическим,
2) векторным.
1) По заданным длинам сторон треугольника АВС находим углы:
cos A= (АВ²+АС²-ВС²)/(2*АВ*АС) = 0,018182.
A = 1,552614 радиан = 88,9582 градусов.
cos В= (АВ²+ВС²-АС²)/(2*АВ*ВС) = 0,4.
B = 1,159279 радиан = 66,42182 градусов.
cos C= (АC²+ВС²-АВ²)/(2*АC*ВС) = 0,909091.
C = 0,4297 радиан = 24,61998 градусов.
Заданный отрезок ХУ рассмотрим как основание трапеции ВХУС.
ХУ = 12 - 5*cos(B/2)*cos(B/2) + 5*cos(B/2)*sin(B/2)*tg(C/2).
Подставив значения функций углов, находим: ХУ = 9.
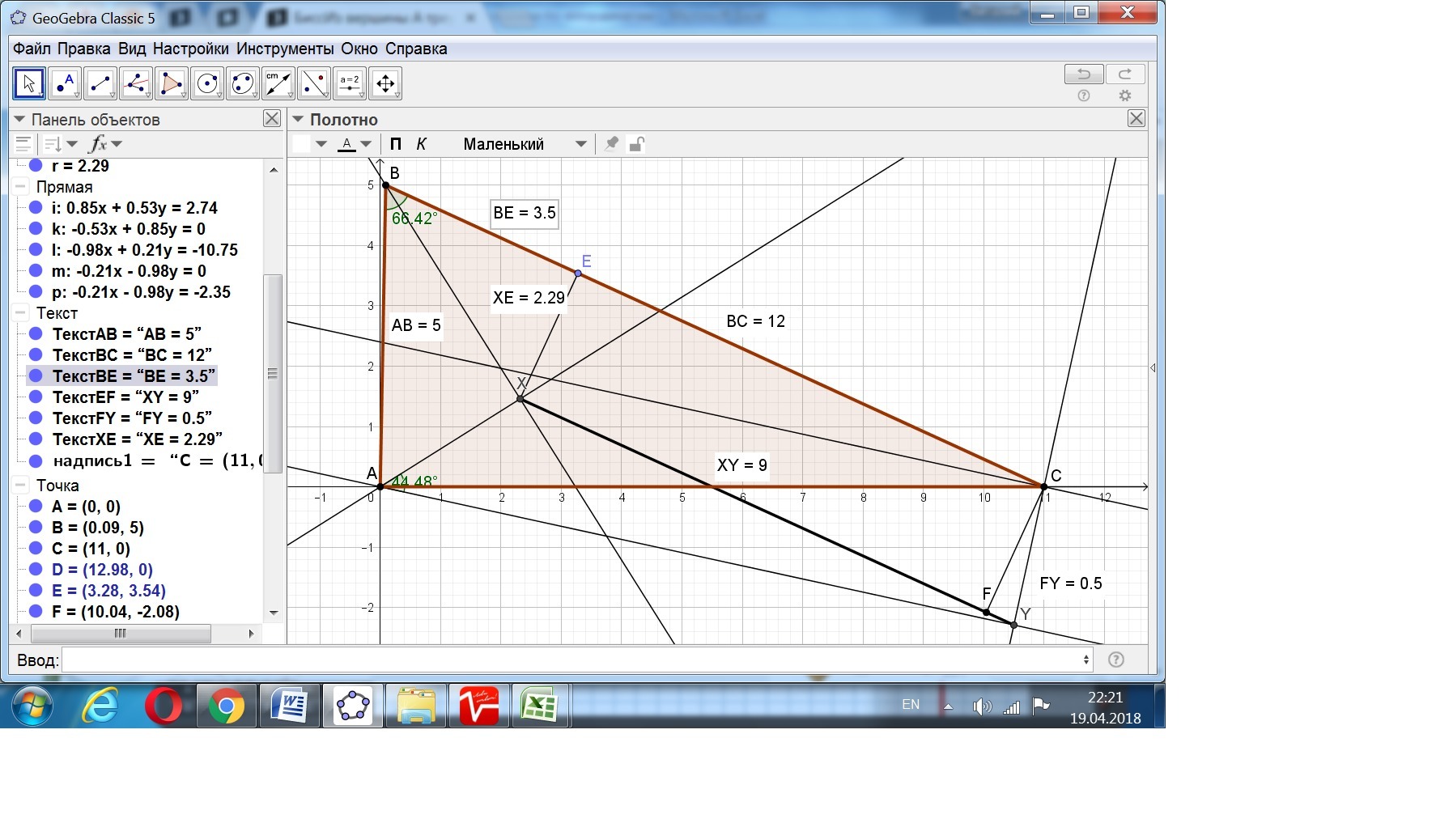
2) Рассмотрим треугольник АВС в системе координат: точка А - начало, точка С -на оси Ох.
С учётом найденных значений углов, определяем координаты вершин:
Точка А Точка В Точка С
Ха Уа Хв Ув Хс Ус
0 0 0,090909 4,999173 11 0
Используем формулу биссектрисы по координатам вершин и длинам сторон: ВХ: ((Уа-Ув + Ус-Ув )/АВ) * Х + ((Хв-Ха + Хв-Хс )/ВС) * У + ((Ха*Ув - Хв*Уа)/АВ + (Хс*Ув - Хв*Ус)/ВС) = 0.
Подставив значения, получаем ВХ в виде уравнения с угловым коэффициентом: у(ВХ) = -1,5898732 х + 5,143707.
Уравнение перпендикуляра АХ из точки А на эту биссектрису с учётом к(АХ) = -1/к(ВХ) : у(АХ) = 0,628980978х.
Находим координаты точки Х как точки пересечения прямых АХ и ВХ
x(Х) = 2,318182; у(Х) = 1,4580923.
Аналогично находим координаты точки У:
x(У) = 10,5; y(У) = -2,2912878.
Теперь длина ХУ равна:
ХУ = √((x(Х)-x(У))²+(у(Х)-у(У))²) = 9.
Из вершины A треугольника ABC опущены перпендикуляр AX на биссектрису угла B и перпендикуляр AY на биссектрису внешнего угла C.
Найти длину отрезка ХУ.
Данную задачу можно решить двумя способами:
1) геометрическим,
2) векторным.
1) По заданным длинам сторон треугольника АВС находим углы:
cos A= (АВ²+АС²-ВС²)/(2*АВ*АС) = 0,018182.
A = 1,552614 радиан = 88,9582 градусов.
cos В= (АВ²+ВС²-АС²)/(2*АВ*ВС) = 0,4.
B = 1,159279 радиан = 66,42182 градусов.
cos C= (АC²+ВС²-АВ²)/(2*АC*ВС) = 0,909091.
C = 0,4297 радиан = 24,61998 градусов.
Заданный отрезок ХУ рассмотрим как основание трапеции ВХУС.
ХУ = 12 - 5*cos(B/2)*cos(B/2) + 5*cos(B/2)*sin(B/2)*tg(C/2).
Подставив значения функций углов, находим: ХУ = 9.
2) Рассмотрим треугольник АВС в системе координат: точка А - начало, точка С -на оси Ох.
С учётом найденных значений углов, определяем координаты вершин:
Точка А Точка В Точка С
Ха Уа Хв Ув Хс Ус
0 0 0,090909 4,999173 11 0
Используем формулу биссектрисы по координатам вершин и длинам сторон: ВХ: ((Уа-Ув + Ус-Ув )/АВ) * Х + ((Хв-Ха + Хв-Хс )/ВС) * У + ((Ха*Ув - Хв*Уа)/АВ + (Хс*Ув - Хв*Ус)/ВС) = 0.
Подставив значения, получаем ВХ в виде уравнения с угловым коэффициентом: у(ВХ) = -1,5898732 х + 5,143707.
Уравнение перпендикуляра АХ из точки А на эту биссектрису с учётом к(АХ) = -1/к(ВХ) : у(АХ) = 0,628980978х.
Находим координаты точки Х как точки пересечения прямых АХ и ВХ
x(Х) = 2,318182; у(Х) = 1,4580923.
Аналогично находим координаты точки У:
x(У) = 10,5; y(У) = -2,2912878.
Теперь длина ХУ равна:
ХУ = √((x(Х)-x(У))²+(у(Х)-у(У))²) = 9.
Приложения:
Похожие вопросы
Предмет: Математика,
автор: arapovalm
Предмет: Другие предметы,
автор: sssroma
Предмет: Биология,
автор: planshetdoma180
Предмет: Математика,
автор: Fgdshhfsfgvxd
Предмет: Химия,
автор: BiReX