Предмет: Математика,
автор: Аноним
Интеграл:∫(x-1)e³ˣdx
(на фото выделенное красным я не понял,если можно продолжите решение пожалуйста)
Приложения:

Ответы
Автор ответа:
0
Приложения:
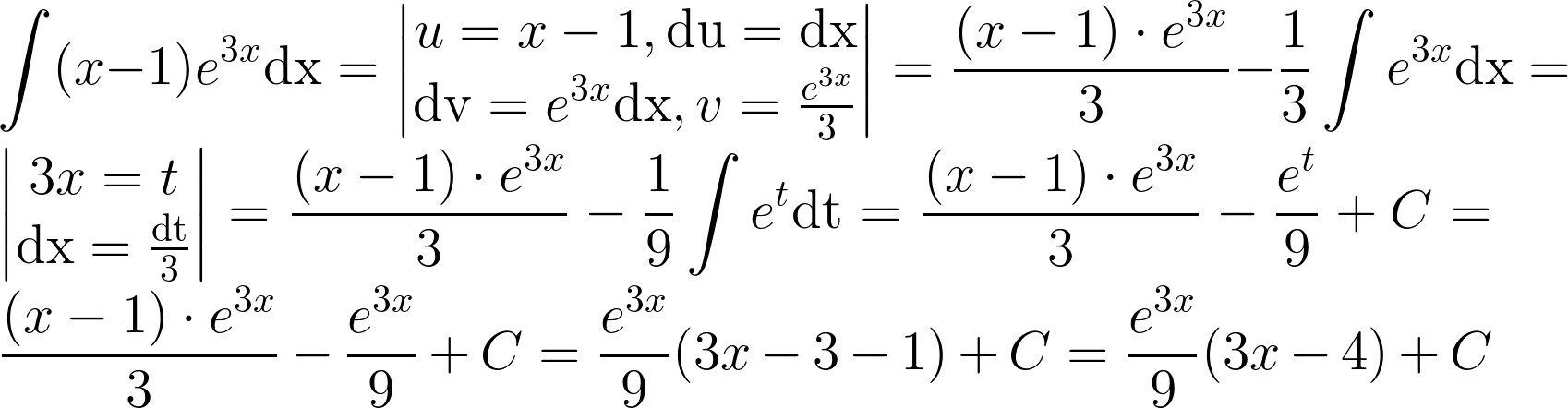
Похожие вопросы
Предмет: Русский язык,
автор: ajsatulintola
Предмет: Русский язык,
автор: mzubenko478
Предмет: Английский язык,
автор: egorburlaj
Предмет: Математика,
автор: ваня548
Предмет: Математика,
автор: 2015елена