Question

Исследуйте функцию с помощью производной и постройте ее график:
f(x)= x^2+3x-4/x+1

Answer 1

ДАНО
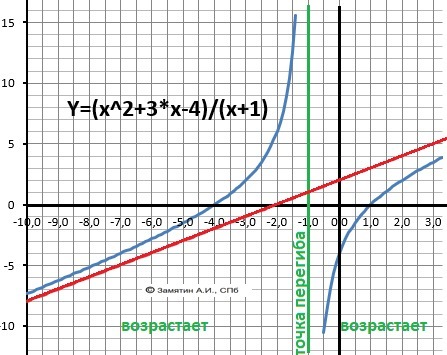
Y=(x²+3*x-4)/(x+1)
ИССЛЕДОВАНИЕ
1. Область определения. Деление на ноль в знаменателе.
Х≠ -1.Х∈(-∞;-1)∪(-1;+∞)
2. Вертикальная асимптота:  Х= -1.
3. Пересечение с осью Х. Y(x) = x²+3*x-4) =(x-1)*(x+4) 
x1 = -4, x2 = 1
4. Пересечение с осью У - Y(0) = - 4
5. Наклонная асимптота 

k = lim(+∞)Y(x)/x = (x²+3*x-4)/(x²+x) = 4. Уравнение асимптоты: Y = x.

6. Проверка на чётность.Y(-x) ≠ Y(x). Y(-x) ≠ - Y(x)

Функция ни четная ни нечетная.
7. Поведение в точке разрыва.
lim(->-1-) Y(x) = +∞. lim(->-1+) Y(x) = -∞. Точка перегиба.

8, Первая производная.

$Y'(x)= \frac{2x+3}{x+1}- \frac{x^2+3x-4}{(x+1)^2}=0$

9. Корней производной - нет. Локальных  экстремумов нет.

10. Участки монотонности функции.
Возрастает на всем интервале определения - Х∈(-∞;+∞).

11. Вторая производная.

$Y"(x)= \frac{2}{x+1}- \frac{2(2x+3)}{(x+1)^2}+ \frac{2*(x^2+3x-4)}{(x+1)^3}$
Корней нет. Точек перегиба (на графике) - нет - разрыв.
12. Выпуклая - "горка" - Х∈(-1;-∞). Вогнутая - "ложка" - Х∈(-∞;-1)

13. График в приложении