Помогите, пожалуйста!
Ответы
Ответ:
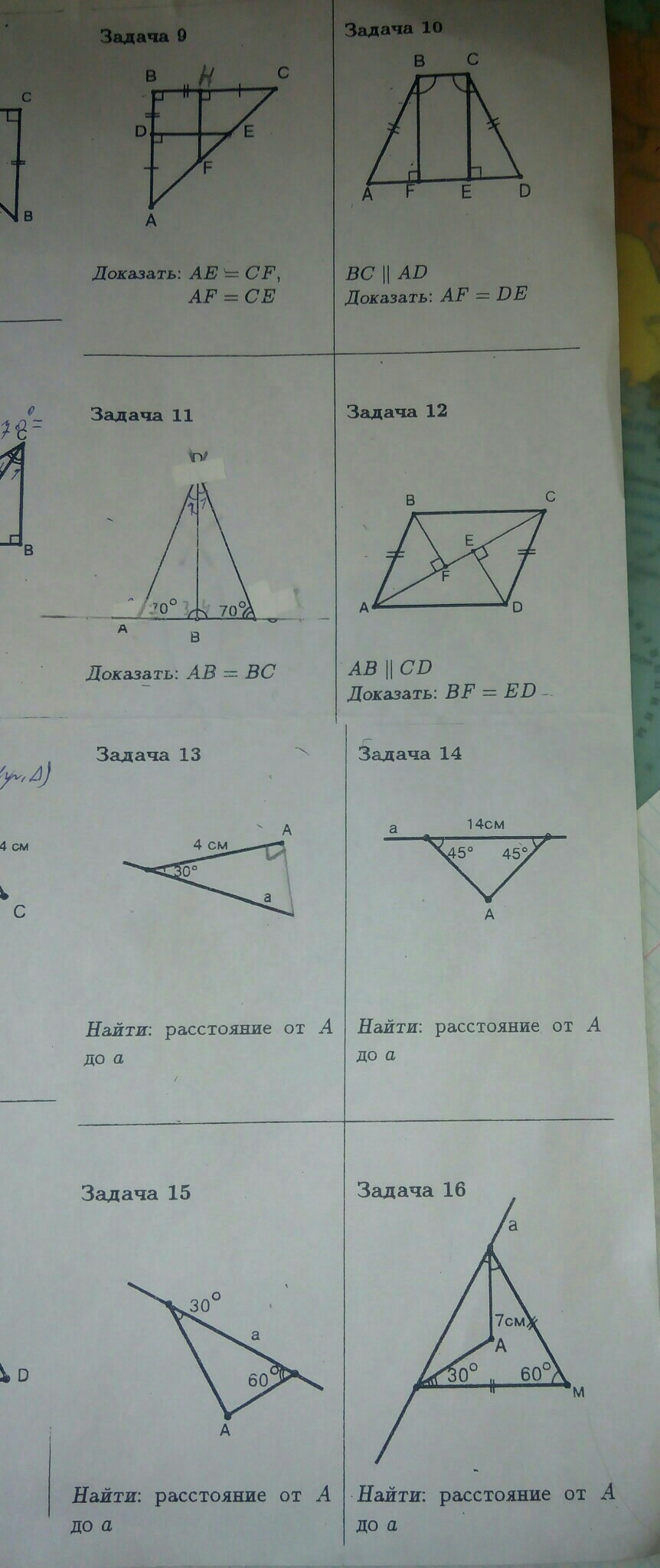
Задача 9.
AB = AD + DB
BC = BH + HC
По условию AD = HC и DB = BH, значит
АВ = ВС, ⇒ ΔАВС прямоугольный равнобедренный, значит
∠А = ∠С = 45°.
∠ADE = ∠CHF = 90°, AD = HC по условию, ∠А = ∠С, значит
ΔADE = ΔCHF по катету и прилежащему углу. Значит
AE = CF.
AF = АЕ - FE
CE = CF - FE, следовательно AF = CE.
Задача 10.
∠BAF = 180° - ∠ABC (внутренние односторонние углы при AD║CB, секущая АВ)
∠CDE = 180° - ∠DCB (внутренние односторонние углы при AD║CB, секущая CD).
∠ABC = ∠DCB по условию, значит и
∠BAF = ∠CDE.
В треугольниках BAF и CDE:
∠BFA = ∠CED = 90°,
∠BAF = ∠CDE (доказано выше),
АВ = CD по условию, значит
ΔBAF = ΔCDE по гипотенузе и острому углу, ⇒
AF = DE.
Задача 11.
Сумма углов треугольника 180°.
ΔABD: ∠ABD = 180° - (∠A + ∠1)
ΔCBD: ∠CBD = 180° - (∠C + ∠1)
Так как ∠А = ∠С по условию, то
∠ABD = ∠CBD, а так как эти углы смежные, то их сумма равна 180°.
∠ABD = ∠CBD = 180° / 2 = 90°.
Итак, в треугольниках ABD и CBD:
∠ABD = ∠CBD = 90°, DB - общая, ∠ADB = ∠CDB по условию, значит
ΔABD = ΔCBD по катету и прилежащему углу, значит
АВ = ВС.
Задача 12.
∠BAF = ∠DCE как накрест лежащие при пересечении АВ║CD секущей АС,
АВ = CD по условию,
∠AFB = ∠CED = 90°, следовательно
ΔAFB = ΔCED по гипотенузе и острому углу, значит
BF = ED.
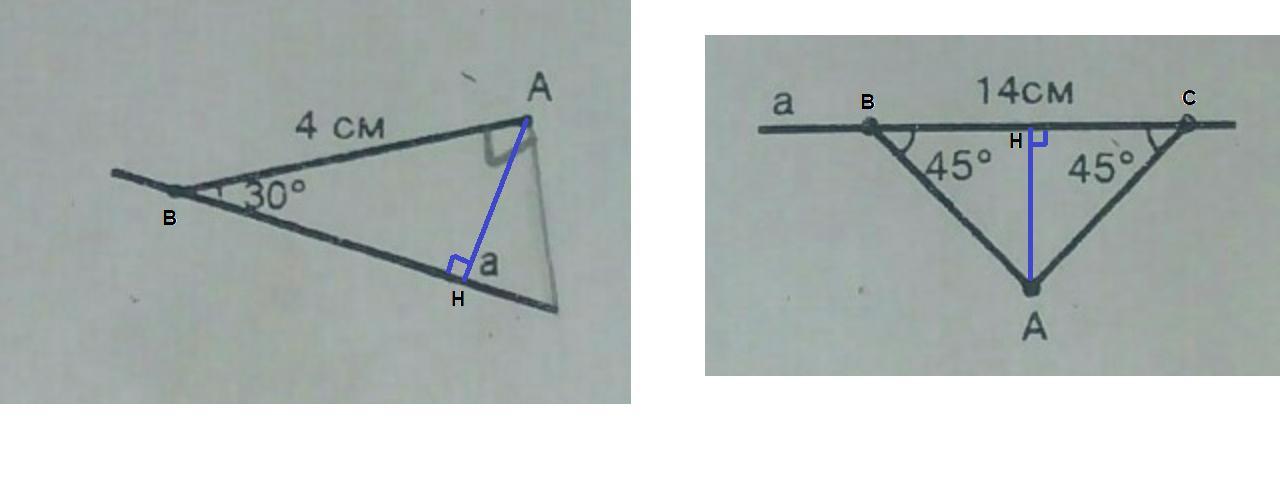
Задача 13.
(см. рисунок)
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к прямой.
Проведем АН⊥а. АН - расстояние от А до а.
ΔАВН: ∠АНВ = 90°,
АН = АВ/2 = 4/2 = 2 см по свойству катета, лежащего против угла в 30°.
Задача 14.
(см. рисунок)
∠АВС = ∠АСВ = 45°, значит ΔАВС равнобедренный (по признаку)
Расстояние от точки до прямой - длина перпендикуляра, проведенного из точки к прямой.
Проведем АН⊥а. АН - расстояние от А до а.
АН - высота равнобедренного треугольника, проведенная к основанию, значит АН - медиана,
ВН = НС = ВС/2 = 14/2 = 7 см
Сумма острых углов прямоугольного треугольника равна 90°.
ΔВАН: ∠ВАН = 90° - 45° = 45°, ⇒ ΔВАН равнобедренный,
АН = ВН = 7 см