Question

ГЕОМЕТРИЯ! СРОЧНО РЕШИТЕ ЗАДАЧУ. ДАЮ 20 БАЛЛОВ!

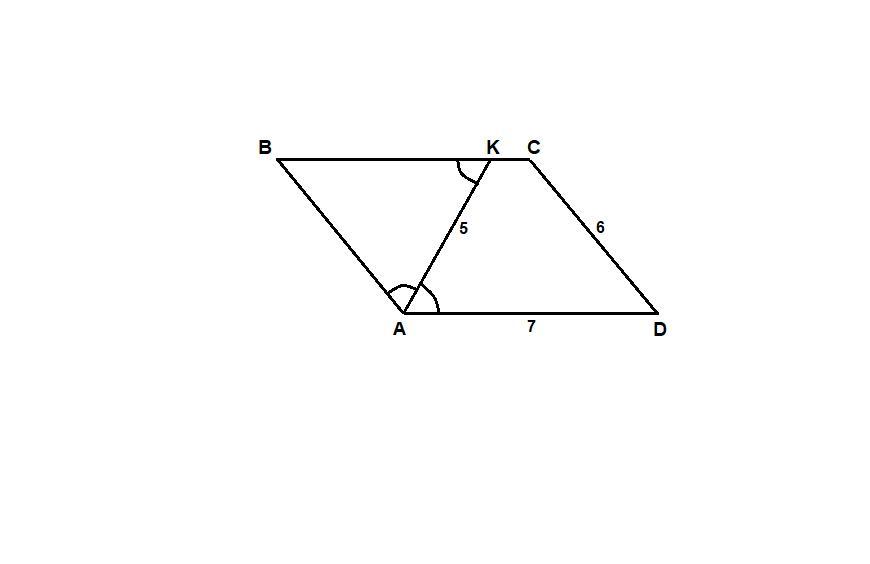
В параллелограмме ABCD проведена биссектриса AK, пересекающая сторону BC в точке K. AD = 7 см, CD = 6 см, AK = 5 см. Найти периметр ADCK.

Answer 1

Ответ:

        Padck = 19 см

Объяснение:

∠ВАК = ∠DAK, так как АК биссектриса,

∠DAK = ∠ВКА как накрест лежащие при пересечении параллельных прямых ВС и AD секущей АК, следовательно

∠ВАК = ∠ВКА, и значит ΔВАК равнобедренный с основанием АК:

АВ = ВК.

Противоположные стороны параллелограмма равны:

АВ = CD = 6 см,  ВК = АВ = 6 см.

КС = ВС - ВК = 7 - 6 = 1 см

Padck = AD + СD + KС + AK = 7 + 6 + 1 + 5 = 19 см