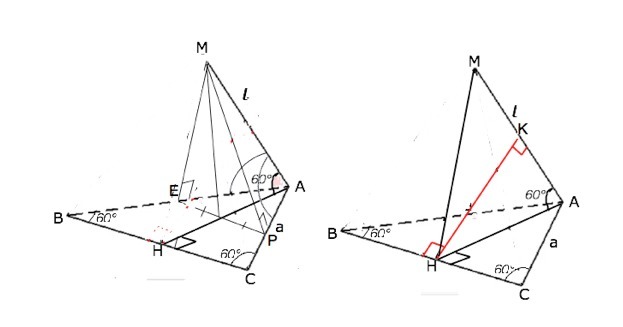
Через вершину А в равностороннем треугольнике АВС проходит прямая l, образующая с плоскостью треугольника угол 60°. Определите расстояние между этой прямой и стороной ВС, если l образует со сторонами АВ и ВС равные углы.
Ответы
Условие исправлено в комментариях.
Через вершину А в равностороннем треугольнике АВС проходит прямая l, образующая с плоскостью треугольника угол 60°. Определите расстояние между этой прямой и стороной ВС, если l образует со сторонами АВ и АС равные углы.–––––––––––––––––
. Поскольку длина стороны ∆ АВС не указана, примем её длину равной а.
Прямая l образует со сторонами АВ и АС равные углы. Отметим на l точку М и опустим из нее на АВ и АС перпендикуляры МЕ и МР.
∆ АЕМ=∆ МРА по гипотенузе и острому углу. Тогда ЕА=АР, отрезок ЕР параллелен ВС и ∆ ЕАР - равносторонний.
МА проецируется на биссектрису АН треугольника АВС. АН - биссектриса, высота, медиана.
Все углы правильного треугольника 60°.
АН=АС•sin60°=а√3/2
Прямая ВС лежит в плоскости ∆ АВС, а прямая l эту плоскость пересекает в точке, не принадлежащей прямой ВС. =>
Прямые АВ и l - скрещивающиеся.
Для нахождения расстояния между прямыми АМ и ВС нужно
провести плоскость, перпендикулярную прямой ВС. Для перпендикулярности заданных прямой и плоскости достаточно, чтобы прямая была перпендикулярна двум пересекающимся прямым, лежащим в этой плоскости.
Прямые МН и АН лежат в плоскости АМН и перпендикулярны ВС. ( АН - перпендикулярна как высота ∆ АВС, МН -по т. о 3-х перпендикулярах- наклонная, чья проекция лежит на АН)
Из точки Н пересечения плоскости АМН с прямой ВС опустим перпендикуляр НК на прямую АМ. Отрезок НК - искомое расстояние.
∆ АКН прямоугольный, угол КАН=60° по условию.
НК=АН•sin60°=а√3/2•√3/2=3а/4
——————
Если длина АВ другая, нужно подставить ее в найденный ответ вместо а.