Предмет: Алгебра,
автор: lquil
Решите уравнение:
пожалуйста, срочно
Приложения:
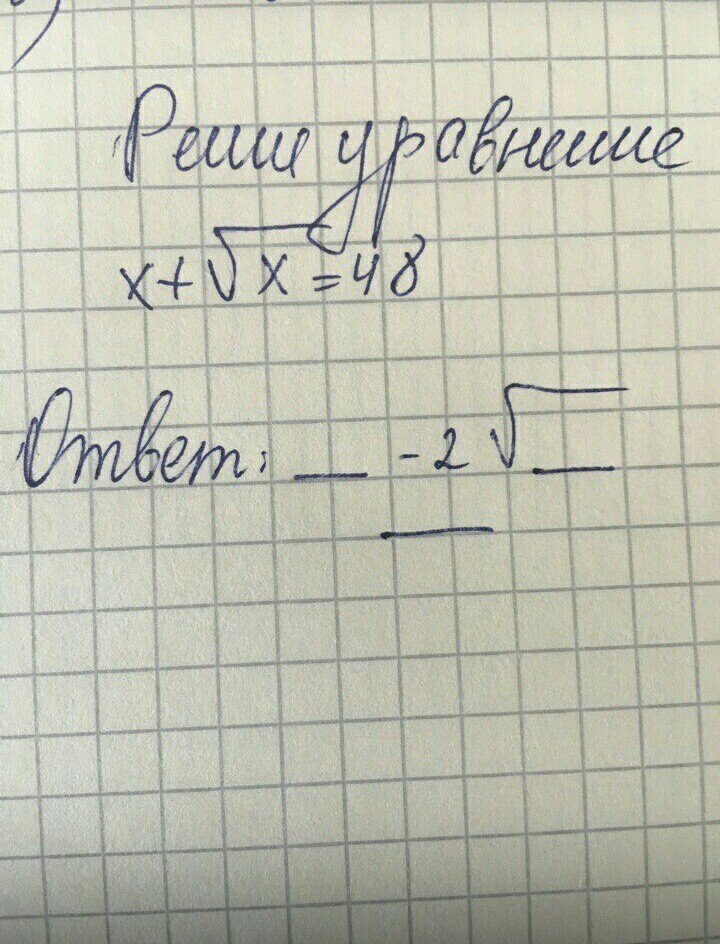
Ответы
Автор ответа:
0
Пусть

Тогда

Вернёмся к замене
 =(194+2✓193)/4
=(194+2✓193)/4
В итоге, корни равны
(194+-2✓193)/4
Тогда
Вернёмся к замене
В итоге, корни равны
(194+-2✓193)/4
Jeltaia:
Некорректно стала отображаться часть решения. Тог написан ниже.
Похожие вопросы
Предмет: Оʻzbek tili,
автор: boriysultonov
Предмет: Математика,
автор: Аноним
Предмет: Алгебра,
автор: DazaiOsamu14
Предмет: Математика,
автор: doc51