Question

Помогите пж ( 8 класс) Касательная окружность

Answer 1

Радиус проведённый к касательной в точку касания, перпендикулярен этой касательной.

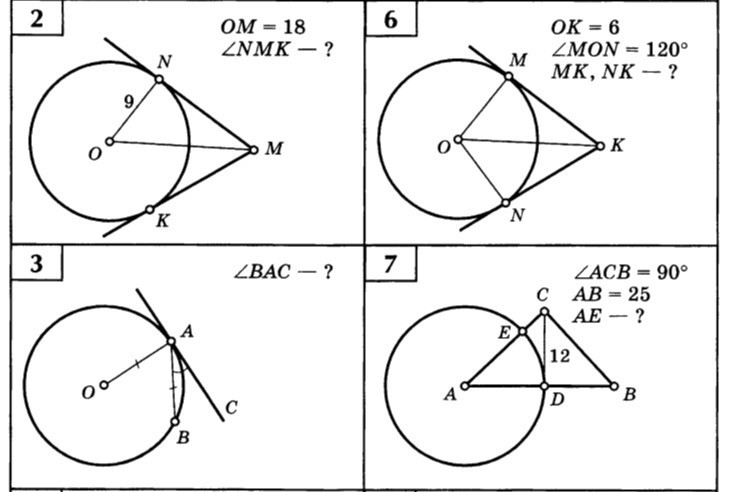
№2.

Прямоугольные треугольники ONM и OKM равны по катету и гипотенузе (∠ONM=90°=∠OKM; ON=9=OK, как радиусы; OM - общая гипотенуза), поэтому ∠OMK=∠OMN.

В ΔONM (∠N=90°): OM=18=2·9=2·ON; угол лежащий напротив катета, который вдвое меньше гипотенузы, равен 30° ⇒ ∠OMN=30°

∠NMK=2·∠OMN=2·30°=60°

Ответ: 60°.

№3.

∠OAC=90°.

ΔOAB - равносторонний (OA=AB по условию и OA=OB, как радиусы), поэтому ∠OAB=60°.

∠BAC=∠OAC-∠OAB=90°-60°=30°

Ответ: 30°.

№6.

ΔOMK=ΔONK по гипотенузе (OK - общая) и катету (OM=ON, как радиусы), откуда ∠KOM=∠KON=120°:2=60° и MK=NK.

В ΔOMK (∠M=90°):

∠K=90°-∠O=90°-60°=30° ⇒ OM=OK:2=6:2=3; По теореме Пифагора:

MK²=OK²-OM²=36-9=27 ⇒ MK=√27=3√3=NK

Ответ: MK=3√3; NK=3√3.

№7.

CD⊥AD как касательная и радиус проведённый в точку касания. AE=AD как радиусы одной окружности.

ΔACD ~ ΔCBD по двум углам (∠CAD=∠BCD и ∠ADC=90°=∠CDB), из подобия следует следующее отношение:

$\dfrac{AD}{CD} =\dfrac{CD}{BD}$

Откуда AD·DB = CD² = 144.

Пусть AD=x, тогда DB = AB-AD = 25-x.

x·(25-x) = 144;

x²-25x+144=0;

x(x-16)-9(x-16)=0;

(x-16)(x-9)=0 ⇒ x₁=16; x₂=9.

Ответ: 9 или 16.

Answer 2

$\boldsymbol{\boxed{\big2}}$

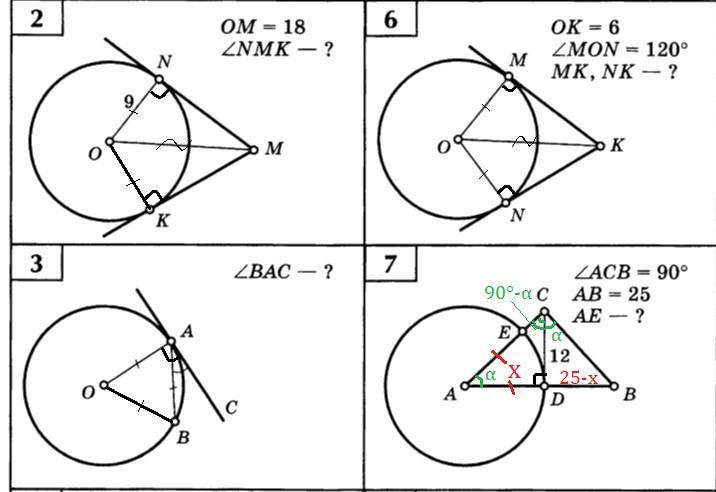
Теорема 1:  Радиус окружности, проведенный в точку касания, перпендикулярен касательной

ON ⊥ MN ,  OK ⊥ MK  

Теорема 2:  Катет прямоугольного треугольника, лежащий против угла 30⁰, равен половине гипотенузы, и наоборот

ON = 9,  OM = 18  ⇒  ∠NMO = 30⁰

OK = 9,  OM = 18  ⇒  ∠KMO = 30⁰

∠NMK = 30⁰ + 30⁰ = 60⁰

$\boxed{\;\Big{Otvet:\;60^o}\;}$

$\boldsymbol{\boxed{\big3}}$

OA = OB - радиусы окружности,    ОА = АВ - по условию

Значит,  OA = OB = АВ  ⇒  Δ АВО - равносторонний

∠АОВ = ∠ОАВ = ∠ОВА = 60⁰

Теорема:  Радиус окружности, проведенный в точку касания, перпендикулярен касательной

OA ⊥ AC  ⇒  ∠OAC = 90⁰

∠BAC = 90⁰ - 60⁰ = 30⁰

$\boxed{\;\Big{Otvet:\;30^o}\;}$

$\boldsymbol{\boxed{\big6}}$

Теорема:  Радиус окружности, проведенный в точку касания, перпендикулярен касательной

OM ⊥ MK ,  ON ⊥ NK

Δ OMK = Δ ONK - по катету и гипотенузе

OM = ON - радиусы окружности,  ОК - общая

∠МОК = ∠NOK = ∠MON : 2 = 120⁰ : 2 = 60⁰

B Δ OMK: sin60⁰ = MK/OK  ⇒  MK = OK *  sin60⁰ = 6 * (√3/2) = 3√3

B Δ ONK: sin60⁰ = MK/OK  ⇒  NK = OK *  sin60⁰ = 6 * (√3/2) = 3√3

$\boxed{\;\Big{Otvet:\;3\sqrt{3}\;;\;3\sqrt{3}\;}}$

$\bolsymbol{\boxed{\big7}}$

AE = AD - радиусы окружности

Теорема:  Радиус окружности, проведенный в точку касания, перпендикулярен касательной

CD ⊥ AB,  AC ⊥ CB

∠СAB = 90⁰ - ∠ABC = ∠BCD

∠ABC = 90⁰ - ∠CAB = ∠ACD

Значит,  Δ ACD подобен Δ BCD по двум углам

AD/CD = CD/BD  ⇒  CD² = AD * BD  ⇒  CD² = AD * (AB - AD)

144 = AD * (25 - AD)   ⇒  AD² - 25AD + 144 = 0 - квадр. уравнение

По теореме, обратной т. Виета:  АD = 9 или AD = 16

$\boxed{\;\Big{Otvet:\;9\;\;ili\;\;16}\;}$