Предмет: Геометрия,
автор: Alex8995
Касательная окружность , помогите пж
Приложения:
Ответы
Автор ответа:
38
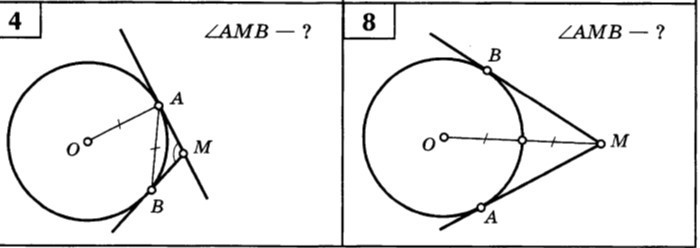
№4.
Дано:
Окр. О;
AM - касательная, AM пересекает Окр. = А;
BM - касательная, BM пересекает Окр. = B;
OA = AB;
Угол AMB - ?
---—
Решение:
Проведём радиус OB. OB = OA = AB, значит, треугольник OAB - равносторонний.
Угол OAB равен углу ABO, равен углу BOA = 180°/3 = 60°.
Т.к. AM - касательная, то угол OAM = 90°, значит, угол BAM = угол OAM - угол OAB = 90° - 60° = 30°.
Аналогично, угол OBM равен 90°, угол ABM = 90° - 60° = 30°.
По теореме о сумме углов треугольника, угол AMB = 180° - 30° - 30° = 120°.
Ответ: угол AMB равен 120°.
№8.
Дано:
Окр. О;
BM и AM - касательные к Окр. из точки М;
OM = 2r;
Угол AMB - ?
---—
Решение:
Проведём радиусы OB и OA.
Sin BMO = OB/OM;
Т.к. OM = 2OB, то Sin BMO = 1/2, значит, угол BMO = 30°.
Известно, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Значит, угол BMO = углу OMA = 30°.
Отсюда, угол AMB = угол BMO + угол OMA,
Угол ABM = 30° + 30° = 60°.
Ответ: угол ABM = 60°.
Дано:
Окр. О;
AM - касательная, AM пересекает Окр. = А;
BM - касательная, BM пересекает Окр. = B;
OA = AB;
Угол AMB - ?
---—
Решение:
Проведём радиус OB. OB = OA = AB, значит, треугольник OAB - равносторонний.
Угол OAB равен углу ABO, равен углу BOA = 180°/3 = 60°.
Т.к. AM - касательная, то угол OAM = 90°, значит, угол BAM = угол OAM - угол OAB = 90° - 60° = 30°.
Аналогично, угол OBM равен 90°, угол ABM = 90° - 60° = 30°.
По теореме о сумме углов треугольника, угол AMB = 180° - 30° - 30° = 120°.
Ответ: угол AMB равен 120°.
№8.
Дано:
Окр. О;
BM и AM - касательные к Окр. из точки М;
OM = 2r;
Угол AMB - ?
---—
Решение:
Проведём радиусы OB и OA.
Sin BMO = OB/OM;
Т.к. OM = 2OB, то Sin BMO = 1/2, значит, угол BMO = 30°.
Известно, что отрезки касательных к окружности, проведённые из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
Значит, угол BMO = углу OMA = 30°.
Отсюда, угол AMB = угол BMO + угол OMA,
Угол ABM = 30° + 30° = 60°.
Ответ: угол ABM = 60°.
Похожие вопросы
Предмет: Английский язык,
автор: lolik3334
Предмет: Химия,
автор: hdhhdhdyhfehfhshs
Предмет: Русский язык,
автор: ilvinasabirzanova151
Предмет: Математика,
автор: лкогкиаш