Предмет: Геометрия,
автор: Kmaj
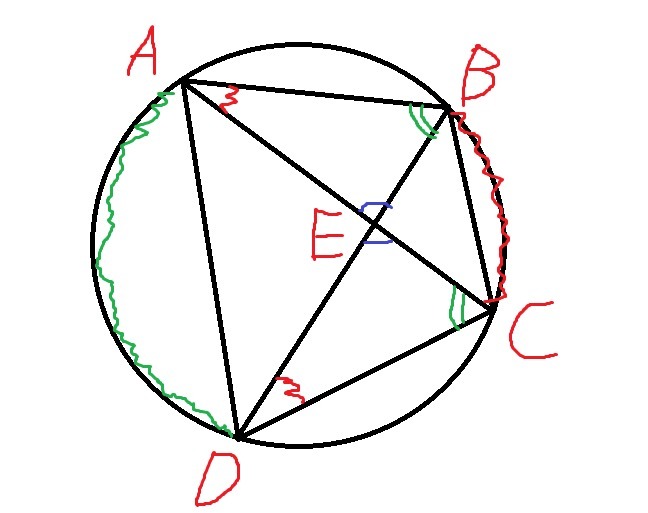
Около четырёхугольника ABCD описана окружность. Диагонали четырёхугольника пересекаются в точке E. Докажите, что треугольники BEA и CED подобны.
Ответы
Автор ответа:
1
Вписанные углы, опирающиеся на одну и ту же дугу, равны, поэтому в этих треугольниках уголABE = уголDCE (опираются на дугу AD) и уголBAE = уголCDE (опираются на дугу BC), треугольники подобны по двум углам
Автор ответа:
3
∠BEA=∠CED (вертикальные)
∠ABD=∠ACD (опираются на одну дугу AD)
∠BAC=∠BDC (опираются на одну дугу BC)
ΔABE подобен ΔDEC (по трём углам)
∠ABD=∠ACD (опираются на одну дугу AD)
∠BAC=∠BDC (опираются на одну дугу BC)
ΔABE подобен ΔDEC (по трём углам)
Приложения:
Похожие вопросы
Предмет: Українська мова,
автор: sofiaprisepa3
Предмет: Математика,
автор: freep6655
Предмет: Алгебра,
автор: angelinamalina20305
Предмет: Литература,
автор: MilkKing
Предмет: Информатика,
автор: narminka12